Содержание
Коэффициент полноты поиска
kotfagot
55
574
0
4816
Коэффициентом полноты поиска (recall ratio) называется такой показатель, который характеризует отношение обнаруженных релевантных документов к общему числу релевантных запросу документов.
Любой потребитель информации (а это каждый из пользователей интернета) заинтересован в рассмотрении только тех документов, которые способны удовлетворить его потребность в сведениях по конкретной теме. Наиболее яркий пример – проверка оригинальности контента. Если найдется хотя бы один документ, подтверждающий, что контент не является оригинальным, дальнейший анализ уже не имеет смысла. Другой пример – поиск наибольшего числа релевантных теме документов, с которыми исследователь должен ознакомиться, прежде чем приступать к научной работе. В этом случае одного документа будет недостаточно.
В этом случае одного документа будет недостаточно.
Способность системы удовлетворить требования пользователя в обоих вышеописанных примерах называется полнотой поиска. Если полнота поиска недостаточна, контент (по первому примеру) будет ошибочно принят за оригинальный – система при проверке просто пропустит схожий документ.
Коэффициент полноты поиска – ключевой показатель поисковой системы. Для вычисления этого показателя используется следующая формула:
ИПС = 100 * (R / C)
В рамках этой формулы литерой R обозначается число обнаруженных релевантных документов, литерой C – общее количество документов, которые имеют отношение к теме запроса.
Допустим, мы знаем, что в системе есть 10 документов, релевантных теме, но в процессе поиска мы сумели обнаружить только 8 из них. В этом случае принято говорить, что коэффициент полноты поиска составляет 80% (8 / 10).
Показателем, обратным коэффициенту полноты поиска, называется коэффициент потери информации, который считается так:
КПИ = 1 – ИПС
По нашему примеру 20% информации оказалось потеряно.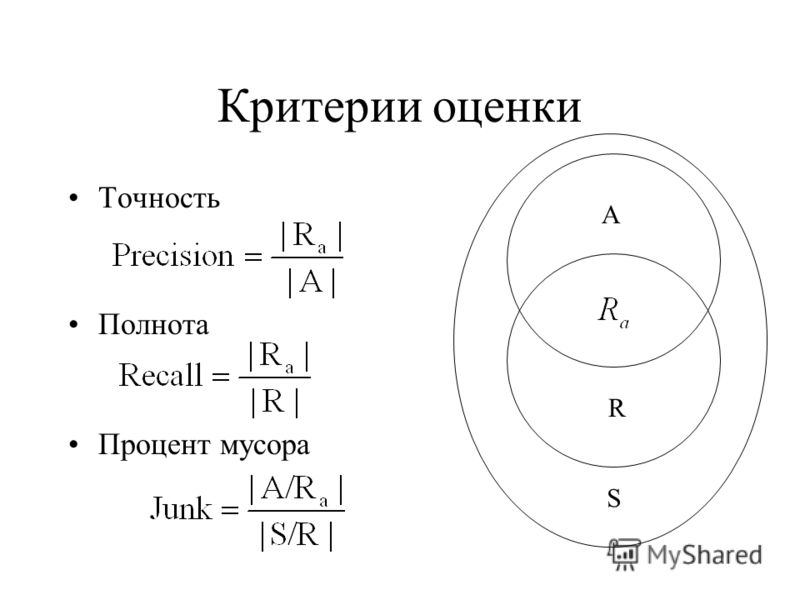
В реальных поисковых системах значение коэффициента полноты поиска, как правило, не выходит за пределы диапазона 0.7 – 0.9.
Нередко по запросу выходят тысячи или даже сотни тысяч релевантных документов, однако, содержание многих из них практически идентично – пользователь может полностью удовлетворить потребность в информации, изучив 2-3 документа, а дальнейшее изучение приведет только к потере времени. В обратной ситуации пользователь может не обнаружить необходимой ему информации даже при высоком значении коэффициента полноты поиска (если тема недостаточно изучена). Все это позволяет считать коэффициент полноты поиска второстепенным показателем, не играющим особой роли при непрофессиональном поиске.
Другим аргументом, подтверждающим невысокую значимость коэффициента полноты поиска, является то, что мы можем добиться 100%-ного значения, вообще не вводя запроса, а последовательно просматривая все имеющиеся в фонде документы.
5.2. Полнота и точность поиска
Коэффициент
полноты– это доля
полученных релевантных документов
посравнению с их общим количеством в
поисковом массиве. Коэффициент точности
Коэффициент точности
это доля релевантных документов среди
выданных.
Введем обозначения
:
a – количество
полученных в результате поиска релевантных
документов,
b – количество
нерелевантных документов, выданных
ИПС,
c – число релевантных
документов в поисковом массиве, не
выданных ИПС,
d – число невыданных
релевантных документов.
Табл. 2 иллюстрирует
подобное разделение документов на
подмножества.
Таблица 2. Разделение
документов в процессе поиска
Тогда коэффициент
полноты1 R и коэффициент точности2 P
можно определить по формулам:
Полнота – англ.
Recall(1). Точность – англ. Precision (2). Выпадение
– англ. Fallout (3). Ошибка – англ. Error (4).
Часто используются
дополнительные меры оценки:
– коэффициент
выпадения(3)F ,
характеризующий количество возвращаемых
системой нерелевантных документов;
– коэффициент
ошибки(4)E, описывающий
правильность определения поисковой
системой релевантности документов:
Если исследовать
эффективность поисковой системы с
помощью нескольких запросов (обозначим
общее число запросов через k), то
для данного запросаiкоэффициенты
полнотыRiи точностиPiможно
записать в виде:
Из приведенных
уравнений можно получить среднюю
величину, которая отражает эффективность
системы, ожидаемую для случая среднего
пользователя. Для этого возьмем среднее
Для этого возьмем среднее
арифметическое по kвыборочным
запросам:
Поскольку значения
коэффициентов полноты Riи точностиPi определяются однозначно для
каждого из запросов пользователей, это
позволяет вычислить средние значения
для фиксированных интервалов полноты.
Кривая, полученная в результате
усреднения, называется кривая
«полнота-точность» поисковой
системы (рис. 12). Левый край этой кривой
соответствует узким, специфичным
формулировкам запросов, а правый —
определяется широкими, общим запросами.
Рис.12. Кривая полнота-точность.
Кривые
“полнота-точность” могут использоваться
для оценки качества работы либо нескольких
ИПС, либо одной, работающей в разных
условиях. При этом кривые, полученные
для двух систем, могут быть наложены на
один график, что позволяет определить,
какая из систем лучше и в какой степени
. Очевидно, что кривая, расположенная
ближе к правому верхнему углу графика
(рис. 12), где полнота и точность максимальны,
12), где полнота и точность максимальны,
указывает на лучшее качество работы.
В идеальной ИПС
коэффициенты полноты и точности равны
единице. В реальных поисковых системах
коэффициент полноты поиска может
достигать значений 0,7 – 0,9, а коэффициент
точности находится в интервале 0,1 – 1,0
.
В дополнение к
стандартным мерам полноты и точности,
значения которых зависят от размера
множества выданных документов, можно
использовать показатели, не зависящие
от выданного множества. В частности,
для систем, в которых полученные документы
ранжируются в порядке уменьшения
сходства между документом и запросом,
существуют меры оценки, основанные на
рангах релевантных документов. Такие
функции, называемые нормализованной
полнотой и нормализованной точностью,
имеют вид:
CSci 4511w: искусственный интеллект
CSci 4511w: искусственный интеллект
Описание большинства алгоритмов поиска в этих заметках взято из
Дж. Перл, «Эвристика», Addison-Wesley, 1984.
Перл, «Эвристика», Addison-Wesley, 1984.
Важные вопросы об алгоритмах поиска
Мы обратимся:
- как писать алгоритмы поиска. В частности, мы рассмотрим:
- структура данных для хранения неисследованных узлов. Мы используем
очередь (часто называемая списком во многих книгах по ИИ) называется OPEN. - расширение узла (или генерация его преемников).
Все потомки узла могут быть сгенерированы одновременно (метод
чаще всего используется) или они могут генерироваться по одному
либо систематически, либо случайным образом.
Число последователей называется коэффициентом ветвления. - стратегий выбора следующего узла для расширения. Разные
алгоритмы являются результатом различных выборов (например, поиск в глубину
когда узлы-преемники добавляются в начало очереди,
в ширину, когда узлы-преемники добавляются в конце
очередь и др.), - тест на цель. Будем предполагать существование предиката
которое применяется к состоянию, вернет true или false.
- бухгалтерия (отслеживание посещенных узлов, отслеживание
путь к цели и др.).
Отслеживание посещенных узлов обычно осуществляется путем сохранения
их в очередь (или, лучше, хеш-таблицу) с именем CLOSED.
Это предотвращает попадание в циклы или повторение работы
но приводит к большой космической сложности. Это (чаще всего)
необходимо при поиске оптимальных решений, но может быть (в основном)
избегать в других случаях.
Отслеживание пройденного пути не всегда необходимо
(когда проблема состоит в том, чтобы найти целевое состояние и знать, как достичь
там не важно).
- структура данных для хранения неисследованных узлов. Мы используем
- свойства алгоритмов поиска и решений, которые они находят:
- Завершение: вычисление гарантировано
завершаться, независимо от того, насколько велико пространство поиска. - Полнота: алгоритм завершен, если он заканчивается
решение, когда оно существует. - Допустимость: алгоритм допустим, если он
гарантирует возврат оптимального решения всякий раз, когда решение существует.
- Пространственная сложность и временная сложность: как размер
памяти, а время, необходимое для запуска алгоритма, растет в зависимости от
по коэффициенту ветвления, глубине решения, количеству узлов и т. д.
Давайте кратко рассмотрим свойства некоторых часто используемых неинформированных
алгоритмы поиска.Поиск в глубину - Завершение:
- гарантируется для конечного пространства, если проверяются повторяющиеся узлы.
Гарантируется при использовании границы глубины.
В противном случае не гарантируется. - Комплектность:
- вообще не гарантируется. Гарантируется, если пространство поиска
является конечным (перебор) и проверяются повторяющиеся узлы. - Допустимость:
- не гарантируется.
Поиск в ширину - Завершение:
- гарантировано для конечного пространства. Гарантируется, когда решение существует.

- Комплектность:
- гарантировано.
- Допустимость:
- алгоритм всегда найдет кратчайший путь
(это может быть не оптимальный путь, если дуги имеют разную стоимость).
Поиск в глубину, итеративное углубление - Завершение:
- гарантировано для конечного пространства. Гарантируется, когда решение существует.
- Полнота:
- гарантировано.
- Допустимость:
- алгоритм всегда найдет кратчайший путь
(это может быть не оптимальный путь, если дуги имеют разную стоимость).
- Завершение: вычисление гарантировано
- классы алгоритмов поиска. Мы можем классифицировать алгоритмы поиска по
несколько измерений. Вот некоторые из наиболее распространенных:- неинформированные (сначала в глубину, в ширину, равномерная стоимость,
ограниченное по глубине, итеративное углубление) по сравнению с информированным (жадным, A*,
ЖДА*, СМА*) - локальный (жадный, стремительный) по сравнению с глобальным (равномерная стоимость, A* и т.
 д.)
д.) - систематический (в глубину, A* и т. д.) против стохастического
(имитация отжига, генетические алгоритмы)
- неинформированные (сначала в глубину, в ширину, равномерная стоимость,
Описание алгоритма неинформированного поиска:
Поиск в глубину с границей глубины
1. Установите начальный узел в положение ОТКРЫТО.
2. пока OPEN не станет пустым или не будет достигнут целевой узел
2.1 удалить самый верхний узел из OPEN и поставить его на
ЗАКРЫТО. Назовите этот узел n.
2.2, если глубина n меньше границы глубины
затем
2.2.1 расширить n, генерируя всех преемников (если есть).
2.2.2 если какой-либо из этих преемников уже включен
путь обхода отбросить его
2.2.3 если любой из этих преемников является целевым узлом,
выход
2.2.4 поместите преемников поверх OPEN и
предоставить для каждого указатель обратно на n
еще
2.2.5 очистка ЗАКРЫТА.
3. Если целевой узел найден,
затем выйдите с решением, полученным путем отслеживания
через его указатели
иначе объявить о неудаче.
Ноты:
- Узлы, которые были расширены (т. е. созданы их преемники)
называются закрытыми, узлы, которые были сгенерированы
и ожидают расширения, называются открытыми. Две очереди, ЗАКРЫТАЯ и ОТКРЫТАЯ
отслеживать эти два набора узлов. - Глубина узла в графе определяется рекурсивно как 1 + глубина его
самый поверхностный родитель. Начальный узел имеет 0 глубины. - Если граница глубины меньше глубины решения, алгоритм
завершается, не найдя решения. Если граница глубины больше
алгоритм может найти неоптимальное решение. Это можно исправить,
завершение поиска до глубины последнего найденного решения, а затем
возврат наилучшего решения. - Для сохранения памяти CLOSED нужно очистить, оставив в ней только
узлов на текущем пути обхода.
Описание алгоритма информированного поиска
Поиск наилучшего первого
Термин «поиск по первому наилучшему» используется по-разному в разных
авторы. Учебник Рассела и Норвига называет поиск наилучших результатов
любой алгоритм, который сортирует
узлы по какой-то функции и каждый раз выбирает лучший.
В Judea Pearl есть несколько иное определение «наилучшего в первую очередь».
дается здесь. Основное различие заключается в спецификации того, как
узлы обработки уже видны (Рассел и Норвиг не указывают, что делать)
и, когда проверка цели завершена (Рассел и Норвиг в Graph-Search проверяют
для гола только на первом элементе OPEN,
Pearl проверяет, как только генерируются преемники узла).
1. Поместите начальный узел S в состояние OPEN.
2. пока OPEN не станет пустым или не будет достигнут целевой узел
2.1 удалить из OPEN узел, в котором f минимально (break
связи произвольно) и поставить его на ЗАКРЫТО. Назовите это
узел н.
2.2 расширить n, генерируя всех преемников (если есть).
2.3 если любой из потомков n является целевым узлом, выйти.
2.4 для каждого преемника n' из n
2.4.1 вычислить f(n')
2.4.2 если n' не было ни OPEN, ни CLOSED, добавить его в
ОТКРЫТЫМ. Прикрепите к нему стоимость f(n').
2.4.3 если n' уже был в состоянии OPEN или CLOSED, сравнить
новое значение f(n') с ранее назначенным
значение f(n'). Если старое значение ниже, отбросить
только что сгенерированный узел. Если новое значение
ниже, замените старый узел новым узлом.
Если старый узел был в состоянии ЗАКРЫТ, переместите его обратно в
ОТКРЫТЫМ.
3. Если целевой узел найден,
затем выйдите с решением, полученным путем отслеживания
через указатели
иначе объявить о неудаче.
Если старое значение ниже, отбросить
только что сгенерированный узел. Если новое значение
ниже, замените старый узел новым узлом.
Если старый узел был в состоянии ЗАКРЫТ, переместите его обратно в
ОТКРЫТЫМ.
3. Если целевой узел найден,
затем выйдите с решением, полученным путем отслеживания
через указатели
иначе объявить о неудаче.
Ноты:
- Шаг 2.3 требует проверки, не расширился ли какой-либо из дочерних элементов узла.
является целевым узлом. Это позволяет завершить работу, как только цель будет найдена, но
возвращаемое решение может иметь большее значение f, чем оптимальное
решение.
Чтобы гарантировать оптимальное решение, нам нужно использовать функцию f, которая
занижает стоимость (как это сделано в A*) и проверяет цель после узла
был выбран для расширения. - Вычисление, необходимое для выполнения тестов, на шаге 2.4.3 может быть
существенный.
Мы могли бы исключить этот шаг за счет необходимости поддерживать
повторяющиеся описания идентичных узлов.
- Если для узла n’, который уже был посещен, найдено меньшее значение
(шаг 2.4.3) и старый узел был ЗАКРЫТ, вместо того, чтобы перемещать его
вернуться к ОТКРЫТОМУ, мы могли бы оставить его ЗАКРЫТЫМ, перенаправить указатель на его
родительский узел (поэтому он будет указывать на нового родителя на более коротком пути) и
пересчитать значения f его потомков. Это требует сохранения
отслеживать потомков узлов, а не только их родителя (так что это делает
программа более сложная для написания), но это экономит повторное расширение узлов, которые
уже расширен (так что это может сэкономить время, если расширение является дорогостоящим
процесс). - В общем случае на функцию f(n) ограничений нет. Лучший первый
всегда выбирает для расширения узел с наименьшим значением f, поэтому f
значения должны быть меньше для лучших узлов. Кроме того, лучший первый отбрасывает
несколько путей, ведущих к одному и тому же узлу, и сохраняет путь с
наименьшее значение f. - Свойства Best-First
- Комплектность:
- гарантируется на конечных пространствах поиска
- Допустимость:
- не гарантируется
- Время Сложность:
- зависит от точности эвристической функции.
 Подробнее см. далее в разделе A*.
Подробнее см. далее в разделе A*. - Космическая сложность:
- O(B в степени d), где B = коэффициент ветвления, а d = глубина решения
А*
1. Поместите начальный узел S в состояние OPEN. Приложите к s стоимость
g(s) = 0. Инициализировать CLOSED пустой очередью.
2. пока OPEN не станет пустым или не будет достигнут целевой узел
2.1 удалить из OPEN узел, в котором f минимально
(произвольно разорвите галстуки) и поставьте его на ЗАКРЫТО.
Назовите этот узел n.
2.2 если n является целевым узлом, выйти.
2.3 расширить n, генерируя всех преемников (если есть).
2.4 для каждого преемника n' из n
2.4.1 вычислить f(n')= g(n') + h(n')
= g(n) + c(n,n') + h(n').
2.4.2 если n' не было ни OPEN, ни CLOSED, добавить
его ОТКРЫТЬ. Прикрепите к нему стоимость f(n').
2.4.3 если n' уже был в состоянии OPEN или CLOSED
направлять его указатели по пути, уступая
самый низкий g(n') и сохранить самый низкий f(n'). 2.4.4 если n' требовала регулировки указателя и была
найдено на ЗАКРЫТО, переместите его обратно на ОТКРЫТО.
3. Если целевой узел найден,
затем выйдите с решением, полученным путем отслеживания
через его указатели
иначе объявить о неудаче.
2.4.4 если n' требовала регулировки указателя и была
найдено на ЗАКРЫТО, переместите его обратно на ОТКРЫТО.
3. Если целевой узел найден,
затем выйдите с решением, полученным путем отслеживания
через его указатели
иначе объявить о неудаче.
Ноты:
- A* — это частный случай поиска по первому наилучшему, где:
- Стоимость f(n) узла вычисляется как f(n) = g(n) + h(n), где
g(n) — стоимость текущего пути от s до n, и
h(n) — оценка стоимости пути от n до цели - Стоимость g узла n вычисляется рекурсивно путем сложения стоимости g узла
его родительский узел m к стоимости дуги от родительского узла m до узла n
g(n) = g(m) + c(m,n).
Мы предполагаем, что стоимость дуги положительна.
Начальный узел имеет стоимость g(s) = 0. - h(n) — недооценка стоимости оптимального пути от n до цели.
Если мы назовем h*(n) стоимость оптимального пути
для всех n h(n) < = h*(n).
Это означает, что целевой узел имеет стоимость h(goal) = 0.
- Стоимость f(n) узла вычисляется как f(n) = g(n) + h(n), где
- Проверка целевого узла (шаг 2.2) должна выполняться после того, как узел
был выбран для расширения, чтобы гарантировать оптимальное решение. - Перенаправление родительского указателя выполняется с использованием только значения g
узел (не значение f). Это гарантирует, что путь, используемый к любому
node — лучший путь. - Когда используемая эвристика монотонна, A* никогда не открывает повторно узлы из ЗАКРЫТОГО.
Это означает, что всякий раз, когда узел помещается в ЗАКРЫТО, A* уже нашел
оптимальный путь к нему. - Если для всех n h(n) = 0, алгоритм A* аналогичен алгоритму Branch&Bound (или
Единая стоимость).
Если для всех n h(n) = 0 и для всех n, n’ c(n,n’)=1, алгоритм A* одинаков
как поиск в ширину. - Свойства А*
- Комплектность:
- гарантируется даже на бесконечных графах при условии, что коэффициент ветвления
конечно и что существует некоторая положительная постоянная дельта такая, что
каждый оператор стоил не меньше дельты.
- Допустимость:
- гарантируется с учетом допустимой эвристики (т. е. h(n) является
недооценка стоимости оптимального пути от n до цели для каждого
узел) - Время Сложность:
- зависит от точности эвристической функции.
Если эвристика
функция точна A* выполняется за линейное время, если эвристическая функция
бесполезно, временная сложность экспоненциальна (как и для единообразной стоимости). - Космическая сложность:
- O(B в степени d)
Итеративное углубление A* (IDA*)
IDA* похожа на итеративное углубление в глубину, разница
являющиеся критерием отсечки. А
путь обрывается, когда общее количество его кроваток f(n) превышает пороговое значение стоимости. ИДА*
начинается с порога, равного f(s) (который равен h'(s), поскольку g(s)
= 0). Каждая итерация — это поиск в глубину
поиск, отсекая ветвь, когда ее значение f(n) превышает пороговое значение.
Если решение найдено, алгоритм завершает работу. В противном случае
порог увеличивается до минимального значения f, превышающего предыдущее
порог, и с нуля начинается еще один поиск в глубину. Этот
Этот
продолжается до тех пор, пока не будет найдено решение.
- Время Сложность:
- зависит от точности эвристической функции. Если эвристика
функция является точной IDA* выполняется за линейное время, если эвристическая функция
бесполезно, временная сложность экспоненциальна (как и для единообразной стоимости). - Космическая сложность:
- О(д)
Эвристические функции
- Эвристическая функция h(n), недооценивающая стоимость
пути от n к цели называется допустимым . - Говорят, что эвристическая функция является монотонной , если для всех пар
узлов n и
n’ (где n’ является преемником n) выполняется следующее неравенство
h(n) < = c(n,n’) + h(n’).
Примеры эвристических функций для головоломки 8
В задаче на 8 головоломок 8 плиток с разными номерами помещаются в 9 ячеек.
места на сетке 3×3. В одном пространстве нет плитки (мы называем его пустым), так что
любая плитка, примыкающая к пустому месту, может быть перемещена, чтобы занять его, сдвинув
от своего исходного положения.
Например, вот начальное и целевое состояния:
начальное состояние целевое состояние 2 8 1 1 2 3 4 6 8 4 7 5 3 7 6 5
Вот несколько различных эвристических функций:
- h2 (n) = количество неуместных плиток
- h3(n) = P(n) + 2 * R(n)
где P(n) — сумма манхэттенских расстояний, от которых находится каждая плитка.
дом,
а R(n) — количество прямых инверсий плитки (когда две соседние плитки
должны быть обменены, чтобы быть в порядке цели). - h4(n) = P(n) + 3 * S(n)
где P(n) — сумма манхэттенских расстояний, от которых находится каждая плитка.
дом,
и S(n) представляет собой оценку последовательности, полученную путем подсчета 1 для центрального
плитка (если не пустая)
и считая 2 за каждую непустую плитку на периметре доски, которая
за ним не следует (по часовой стрелке) его надлежащий преемник.
При вычислении S(n) пустая плитка не учитывается.
Эта эвристика недопустима.
Вот пример того, как вычислить эти эвристики для
начальная конфигурация показана выше.
Значение R(n) равно 0, потому что прямых переворотов тайлов нет.
| P(n) = | S(n) = | ||
| 1 + | (2 — это 1 позиция от ворот) | 2 + | (за 2 не следует его преемник) |
| 2 + | (8 на 2 позиции дальше от ворот) | 0 + | (8, за которой следует его преемник) |
| 2 + | (1 на 2 позиции дальше от ворот) | 2 + | (за 1 не следует его преемник) |
| 2 + | (6 на 2 позиции дальше от ворот) | 2 + | (за 6 не следует его преемник) |
| 2 + | (3 – 2 позиции от ворот) | 2 + | (3, за которым не следует его преемник) |
| 1 + | (5 на 1 позицию дальше от цели) | 2 + | (5, за которым не следует его преемник) |
| 0 + | (7 равно 0 позиции от цели) | 2 + | (за 7 не следует его преемник) |
| 2 = | (4 на 2 позиции от позиции ворот) | 2 = | (4, за которым не следует его преемник) |
| 12 | 14 |
Пустая плитка не считается, даже если она не находится в своей целевой позиции.
В этом случае центральная плитка пуста, поэтому мы не добавляем для нее S(N)1.
Если мы
если бы на границе была пустая плитка, это не повлияло бы на порядковый номер
потому что для вычисления порядкового номера вы смотрите только на пронумерованные
плитка.
Вопрос о полноте в ширину и неполноте в глубину
спросил
Изменено
2 года, 1 месяц назад
Просмотрено
14 тысяч раз
Согласно Норвигу в AIMA (Искусственный интеллект: современный подход), алгоритм поиска в глубину не является полным (не всегда дает решение), потому что бывают случаи, когда спусковое поддерево будет бесконечным.
С другой стороны, подход в ширину называется полным, если коэффициент ветвления не бесконечен. Но разве это не то же самое, что и в случае с бесконечным поддеревом в DFS?
Нельзя ли назвать DFS полной, если глубина дерева конечна? Как же тогда получается, что BFS полна, а DFS нет, если полнота BFS зависит от того, что коэффициент ветвления конечен!
- поиск в глубину
- поиск в ширину
Дерево может быть бесконечным без бесконечного коэффициента ветвления. В качестве примера рассмотрим дерево состояний для кубика Рубика. При заданной конфигурации куба существует конечное число ходов (я полагаю, 18, поскольку ход состоит в выборе одного из 9 кубиков).»плоскости» и вращая его в одном из двух возможных направлений). Однако дерево бесконечно глубоко, поскольку вполне возможно, например, только вращайте одну и ту же плоскость попеременно вперед и назад (никогда не добиваясь никакого прогресса). Чтобы предотвратить это от DFS, обычно кэшируются все посещенные состояния (эффективно обрезая дерево состояний) — как вы, вероятно, знаете. Однако, если пространство состояний слишком велико (или фактически бесконечно), это не поможет.
В качестве примера рассмотрим дерево состояний для кубика Рубика. При заданной конфигурации куба существует конечное число ходов (я полагаю, 18, поскольку ход состоит в выборе одного из 9 кубиков).»плоскости» и вращая его в одном из двух возможных направлений). Однако дерево бесконечно глубоко, поскольку вполне возможно, например, только вращайте одну и ту же плоскость попеременно вперед и назад (никогда не добиваясь никакого прогресса). Чтобы предотвратить это от DFS, обычно кэшируются все посещенные состояния (эффективно обрезая дерево состояний) — как вы, вероятно, знаете. Однако, если пространство состояний слишком велико (или фактически бесконечно), это не поможет.
Я не изучал ИИ подробно, но предполагаю, что обоснование того, что BFS является полным, а DFS — нет (в конце концов, полнота — это просто термин, который где-то определен) заключается в том, что бесконечно глубокие деревья встречаются чаще, чем деревья с бесконечными факторами ветвления (поскольку наличие бесконечного фактора ветвления означает, что у вас есть бесконечное количество вариантов выбора, что, я считаю, не является обычным явлением — игры и симуляции обычно дискретны). Даже для конечных деревьев BFS обычно работает лучше, потому что DFS, скорее всего, начнет с неправильного пути, исследуя большую часть дерева, прежде чем достичь цели. Тем не менее, как вы указываете, в конечном дереве DFS в конце концов найдет решение, если оно существует.
Даже для конечных деревьев BFS обычно работает лучше, потому что DFS, скорее всего, начнет с неправильного пути, исследуя большую часть дерева, прежде чем достичь цели. Тем не менее, как вы указываете, в конечном дереве DFS в конце концов найдет решение, если оно существует.
5
DFS не может зацикливаться (если у нас есть список открытых и закрытых состояний). Алгоритм не завершен, так как он не находит решения в бесконечном пространстве, хотя решение находится в глубине d , что намного меньше бесконечности.
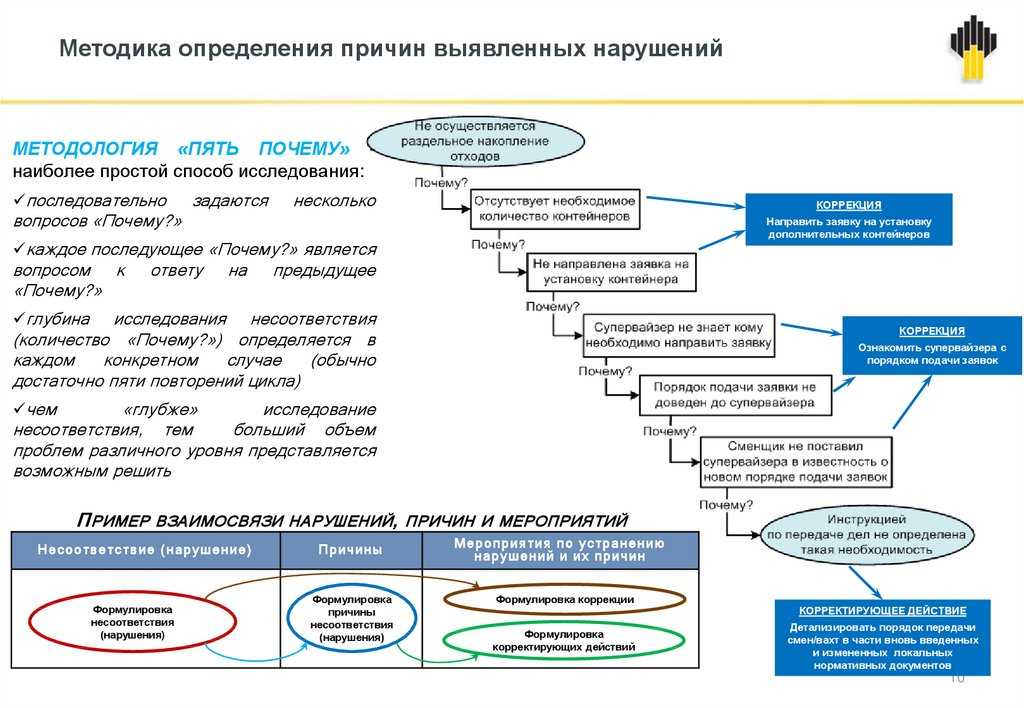
Представьте себе странно определенное пространство состояний, в котором каждый узел имеет такое же количество последователей, как и следующее число в последовательности Фибоначчи. Итак, он рекурсивно определен и, следовательно, бесконечен. Мы ищем узел 2 (отмечен зеленым на графике). Если DFS начинается с правой ветви дерева, потребуется бесконечное количество шагов, чтобы убедиться, что нашего узла там нет.



 д.)
д.)
 Если старое значение ниже, отбросить
только что сгенерированный узел. Если новое значение
ниже, замените старый узел новым узлом.
Если старый узел был в состоянии ЗАКРЫТ, переместите его обратно в
ОТКРЫТЫМ.
3. Если целевой узел найден,
затем выйдите с решением, полученным путем отслеживания
через указатели
иначе объявить о неудаче.
Если старое значение ниже, отбросить
только что сгенерированный узел. Если новое значение
ниже, замените старый узел новым узлом.
Если старый узел был в состоянии ЗАКРЫТ, переместите его обратно в
ОТКРЫТЫМ.
3. Если целевой узел найден,
затем выйдите с решением, полученным путем отслеживания
через указатели
иначе объявить о неудаче.

 Подробнее см. далее в разделе A*.
Подробнее см. далее в разделе A*. 2.4.4 если n' требовала регулировки указателя и была
найдено на ЗАКРЫТО, переместите его обратно на ОТКРЫТО.
3. Если целевой узел найден,
затем выйдите с решением, полученным путем отслеживания
через его указатели
иначе объявить о неудаче.
2.4.4 если n' требовала регулировки указателя и была
найдено на ЗАКРЫТО, переместите его обратно на ОТКРЫТО.
3. Если целевой узел найден,
затем выйдите с решением, полученным путем отслеживания
через его указатели
иначе объявить о неудаче.