Проверка Возраста Домена (DA) Сайта

Завершение вашего присутствия в Интернете путем выбора правильного доменного имени — один из наиболее важных аспектов создания вашего бренда в Интернете. Однако иногда может быть трудно определить, какие домены будут существовать в долгосрочной перспективе, а какие могут скоро исчезнуть. Вот где пригодятся средства проверки возраста домена; Этот тип инструмента позволяет легко узнать, насколько старым на самом деле является данное доменное имя, помогая вам определить потенциально неправильный выбор, прежде чем вы совершите его.

Что такое средство проверки возраста домена?

Инструмент проверки возраста домена — отличный инструмент для тех, кто хочет приобрести доменное имя. Это позволяет вам увидеть, сколько лет доменному имени на самом деле и когда истечет срок его действия. Используя средство проверки возраста домена, вы можете убедиться, что покупаете действительный и активный домен для своего бизнеса.

Перед размещением заказа существует несколько способов проверить доменные имена. Если вам нужно проверить возраст веб-сайта, вы можете использовать массовую проверку возраста домена. Вы также можете использовать средство проверки срока действия домена, чтобы узнать, когда он истекает. В дополнение к этому можно использовать средство проверки даты регистрации домена, чтобы выяснить, когда был создан веб-сайт.

Перед покупкой старого домена вы должны получить информацию о времени его создания, его репутации, используемых стратегиях SEO и его трафика — аналогично тому, что вы делаете при покупке подержанного автомобиля. Инструменты проверки возраста домена, как правило, отображают даты регистрации, обновления и истечения срока действия вашего доменного имени. Также рекомендуется проверить IP-адрес, имя сервера или хостинговой компании, историю веб-архива и т. д.

Использование средства проверки возраста домена

Шаг 1. Вставьте свой домен

Просто введите URL своего веб-сайта и нажмите на стрелку, чтобы получить результаты.

Шаг 2. Анализ результатов проверки возраста домена

Программное обеспечение будет запускать ваш веб-сайт через свою систему, чтобы показать вам, когда домен был создан, когда он был обновлен и когда истекает срок его действия.

Что такое возраст домена?

Возраст домена — это приблизительная оценка того, сколько лет веб-сайту или веб-странице. Веб-сайт, который существует уже несколько лет, будет иметь более старый домен, чем недавно зарегистрированный. Владельцы веб-сайтов могут использовать эти инструменты, чтобы проверить свои собственные домены и узнать, как долго они существуют. Срок действия регистрации доменного имени истекает через определенный период времени, и вам необходимо продлить ее, чтобы продолжать ее использовать.

Возраст домена также помогает определить, может ли кто-то еще заинтересоваться регистрацией вашего доменного имени до истечения срока его действия, чтобы они могли получить право собственности на него от вас. Более того, это помогает вам решить, когда может потребоваться приобрести другое доменное имя, чтобы вам не пришлось полностью закрыть свой сайт из-за истечения срока действия вашего текущего доменного имени.

Важен ли возраст домена для SEO?

Это оказывает некоторое влияние на вашу SEO-статистику. Давайте углубимся в тему.

Что говорит Google?

Как правило, Google учитывает два фактора, чтобы определить возраст домена. Первый фактор — это частота обновления контента на сайте и время последнего обновления. Google должен видеть, что вы активно обновляете свой веб-сайт, регулярно добавляя новый контент. То, как часто обновляется сайт, также оказывает влияние: если вы годами не добавляете свежих сообщений, Google может сделать вывод, что вы забросили свой сайт. В конце концов, зачем продолжать платить за веб-хостинг, если нет страниц для загрузки? Что касается того, сколько раз в год вы должны обновлять контент на своих сайтах, мы рекомендуем делать это от 3 до 5 раз в год или даже чаще, в зависимости от типа сайтов.

Преимущества старых DA для SEO

Качественные обратные ссылки — одна из основных причин, по которой старые домены лучше ранжируются в поисковых системах. Поисковые системы изучают обратные ссылки, обращая особое внимание на доминирование сайтов, и, если они авторитетны, эти сайты оцениваются выше. Работаем над строительством кв.

Наличие обратных ссылок для сайта было бы огромным преимуществом.

Еще одним преимуществом старых доменов является то, что они обычно имеют хорошую репутацию в своей нише. Это приятное преимущество, потому что создание солидной репутации поначалу требует много времени и усилий. Если у вас есть возможность приобрести старый домен с хорошей репутацией и высоким рейтингом в поисковой выдаче, считайте, что вам крупно повезло. Многие предприятия вкладывают годы и значительные суммы денег, чтобы создать хорошую репутацию и надежность.

Старые домены также получают много трафика. Стабильный трафик стоит денег, времени и работы; таким образом, покупка старого домена с ранее установленным значительным трафиком является огромным бонусом. Все, что вам нужно сделать сейчас, это поддерживать текущий уровень трафика, работая над его увеличением.

Целью любого SEO-менеджера является вывести свои сайты на вершину страниц результатов поисковых систем; поэтому, если сайт уже имеет хороший рейтинг в поисковых системах, вы, несомненно, сэкономите деньги и время. Конечная цель — добиться высокого рейтинга вашего веб-сайта, а высший рейтинг является синонимом прибыли и видимости.

С учетом сказанного, есть некоторые вещи, о которых вам нужно быть осторожным при покупке старых доменов. Некоторые владельцы сайтов и веб-мастера используют различные черные методы SEO, чтобы получить более высокий рейтинг для своего домена. Вы должны изучить веб-сайт с точки зрения этой проблемы и поработать над ее удалением, иначе сайт окажется под угрозой. Кроме того, у некоторых старых доменов плохая репутация. Если предыдущие пользователи заблокировали этот сайт или пометили его как спам, значит, вы получите сайт с запятнанной репутацией, который может навредить вашему бизнесу.

Проверка возраста домена важна, но недостаточна для получения хороших позиций в поисковой выдаче!

Теперь вы знаете об возрасте домена, а дальше — просканируйте свой сайт и выясните всевозможные проблемы, которые могут повредить вашим пользователям или SEO вашего сайта.

Как и где найти устаревшие домены

Чтобы найти устаревший домен по возрасту, просто используйте инструмент проверки возраста домена. Как правило, домены возрастом от 10 лет и выше имеют высокий авторитет и SEO. Вы можете купить домен только после истечения срока его действия, поэтому убедитесь, что дата соответствует вашим потребностям. Однако перед покупкой обязательно проверьте его репутацию и историю спама. Все доступные доменные имена можно купить на аукционах на онлайн-рынках и веб-сайтах.

Часто задаваемые вопросы

Можете ли вы стать владельцем домена до 18 лет?

Согласно ICANN (Интернет-корпорация по присвоению имен и номеров), если вам меньше 18 лет, вы не можете регистрировать какие-либо доменные имена или имена хостов.

Можете ли вы купить домен без ежегодной оплаты?

Да, вы можете купить домен без ежегодной оплаты. Регистрация доменного имени выполняется один раз в год. Это означает, что вам придется вносить предоплату на срок до десяти лет, чтобы гарантировать, что у вас будет доменное имя. в течение десяти лет.

Безопасны ли домены Google?

Да, Google Domains безопасен. Он предлагает бесплатную защиту конфиденциальности, DNSSEC одним щелчком мыши и двухэтапную проверку Google для любого регистрируемого вами домена.

Какой возраст должен быть у домена?

Домен возрастом от десяти лет и более имеет высокие шансы иметь большой профиль обратных ссылок и некоторую фактическую силу рейтинга за качественным контентом.

ᐉ Узнать возраст домена в 1 клик

Сервис позволит узнать сколько лет домену сайта

Ошибка. Попробуйте другое доменое имя.

Whois данные домена

WHOIS проверка домена разработана специалистами HyperHost.UA

Хостинг для сайтов

• Бесплатный домен
• Бесплатный SSL
• Бесплатный перенос
• Поддержка PHP и MySQL

Перейти

VPS сервера

• Бесплатная поддержка
• KVM или OpenVZ
• Выделенный IP
• Полный root доступ

Перейти

Физические сервера

• Администрирование 24/7
• Бесплатная тех.поддержка
• Помощь с переносом
• Аудит и оптимизация

Перейти

Регистрация Доменов

• 200 доменных зон
• Домены в подарок
• Скидки до 15%
• Срок регистрации до 10 лет

Перейти

Данный сервис позволяет проверить любой зарегистрированный домен на возраст. Возрастом домена принято считать количество лет, месяцев и дней с дня регистрации домена. Важно понимать, что возраст домена указывает только время безперерывной работы домена. Если домен был зарегистрирован в период с 2000 по 2010, а потом с 2016 года по сегодня, возраст домена будет считаться только последний проимежуток активного использования домена.

Как работает сервис?
Данный инструмент проверки доменного имени берет за основу дату регистрации домена и отсчитывает количество дней до времени проверки. Вы можете сделать это самостоятельно с помощью инструмента WHOIS проверки домена. Все, что вам нужно, взять в основу рассчетов дату из поля «created» и рассчитать возраст самостоятельно.

Знать возраст доменов необходимо в некоторых случаях:

• при размещении обратных ссылок на сайт важно знать трастовость анализируемого сайта, возраст напрямую влияет на этот показатель;
• возраст домена позволяет отличить мошеннический сайт, так сотни доменов регистрируются специально на несколько дней ради совершения мошеннических действий;
• в случае покупки сайта с рабочим доменом, проверка возраста домена сайта является важной частью определения ценности такого сайта.

В целом данный сервис позволяет значительно упростить процесс определения возраста домена.

Анализ во временной области и анализ в частотной области: руководство и сравнение

Слово «анализ» вызывает как провокации мысли, так и представляет собой воплощение просветления с точки зрения понимания. По сути, это процесс, посредством которого мы обнаруживаем или получаем лучшее понимание человека, места или предмета. Более того, именно наши аналитические способности обычно обеспечивают нашу безопасность, если мы действительно их используем. Я вспоминаю случай, когда мой лучший школьный друг не смог провести надлежащий анализ, несмотря на то, что видел все предупреждающие знаки. Экспонат А, большая собачья миска, наполовину полная. Экспонат B, большая табличка «Остерегайтесь собак». Наконец, экспонат C, передний двор полностью огорожен.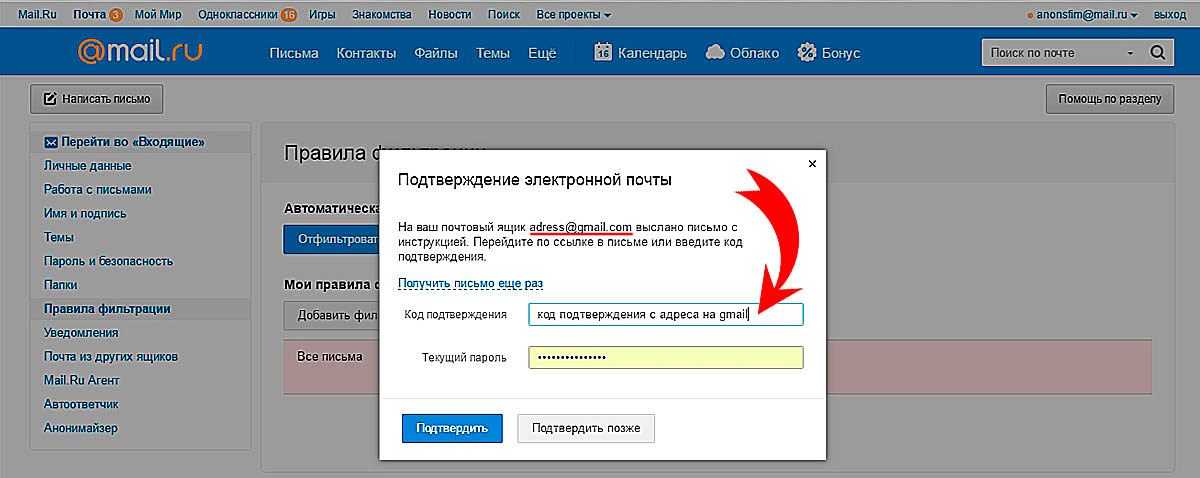

Однако, несмотря на мои предупреждения и множество хорошо заметных предупреждающих знаков, он решает открыть ворота и попытаться выполнить свою квоту (сбор средств на обмундирование). Когда я стал свидетелем этой катастрофы, которая ждала своего часа, сидя на своем 21-скоростном шоссейном велосипеде, она произошла. Это было похоже на сцену из Куджо, за исключением того, что она казалась замедленной, как Матрица. Излишне говорить, что он не был «Единственным».

Я начинаю крутить педали изо всех сил, но слышу сзади несколько криков, за которыми следует интенсивное рычание добермана. К счастью, никто не пострадал, если не считать боли в животе от всего этого смеха. Однако отказ от использования инструментов анализа в электронике почти всегда вреден. Возьмем, к примеру, анализ во временной области и анализ в частотной области; это два таких инструмента, которые при правильном использовании могут обеспечить бесценную информацию о сигналах.

Что такое анализ во временной области?

Анализ во временной области представляет собой анализ физических сигналов, математических функций или временных рядов экономических или экологических данных по отношению ко времени. Кроме того, во временной области значение сигнала или функции понимается для всех действительных чисел в различных отдельных случаях в случае дискретного времени или в случае непрерывного времени. Кроме того, осциллограф — это инструмент, обычно используемый для просмотра реальных сигналов во временной области.

Кроме того, график во временной области может показать, как сигнал изменяется во времени, тогда как график в частотной области покажет, какая часть сигнала находится в пределах каждой заданной полосы частот в диапазоне частот.

В общем, когда в анализе используется единица времени, например, секунды или одно из ее кратных значений (минуты или часы) в качестве единицы измерения, то это относится к временной области. Однако всякий раз, когда анализ касается таких единиц, как герц, он проводится в частотной области.

Чем анализ во временной области отличается от анализа в частотной области?

Частотная область представляет собой анализ сигналов или математических функций по отношению к частоте, а не ко времени. Как указывалось ранее, график во временной области отображает изменения сигнала в течение определенного промежутка времени, а в частотной области показывает, какая часть сигнала присутствует в заданной полосе частот относительно диапазона частот. Кроме того, представление в частотной области может включать в себя информацию о фазовом сдвиге, который необходимо применить к каждой синусоиде, чтобы иметь возможность рекомбинировать частотные компоненты для восстановления исходного временного сигнала.

Кроме того, вы можете преобразовать назначенный сигнал или функцию между частотной и временной областями с помощью пары операторов, называемых преобразованиями. Более того, прекрасным примером преобразования является преобразование Фурье. Который преобразует функцию времени в интеграл синусоид различных частот или сумму, каждая из которых символизирует частотную составляющую. Так называемый спектр частотных составляющих представляет собой изображение сигнала в частотной области. Однако, как следует из названия, обратное преобразование Фурье преобразует функцию частотной области обратно в функцию времени.

Управление сигналами антенны или передачей звука изменит тип используемого анализа.

Нюансы между частотной и временной областью

Анализ во временной области обеспечивает переходную реакцию анализируемой системы и позволяет лучше понять поток как механической, так и электрической энергии. В общем случае сюда входят распространение волн, структурные изменения системы и электрический потенциал, создаваемый внешними возбуждениями.

В то время как для частотной области инструменты визуализации, такие как анализатор спектра, обычно используются при визуализации электронных сигналов. Кроме того, некоторые специализированные методы обработки сигналов используют преобразования, что приводит к совместной частотно-временной области. Более того, мгновенная частота является критическим связующим звеном между временной областью и частотной областью.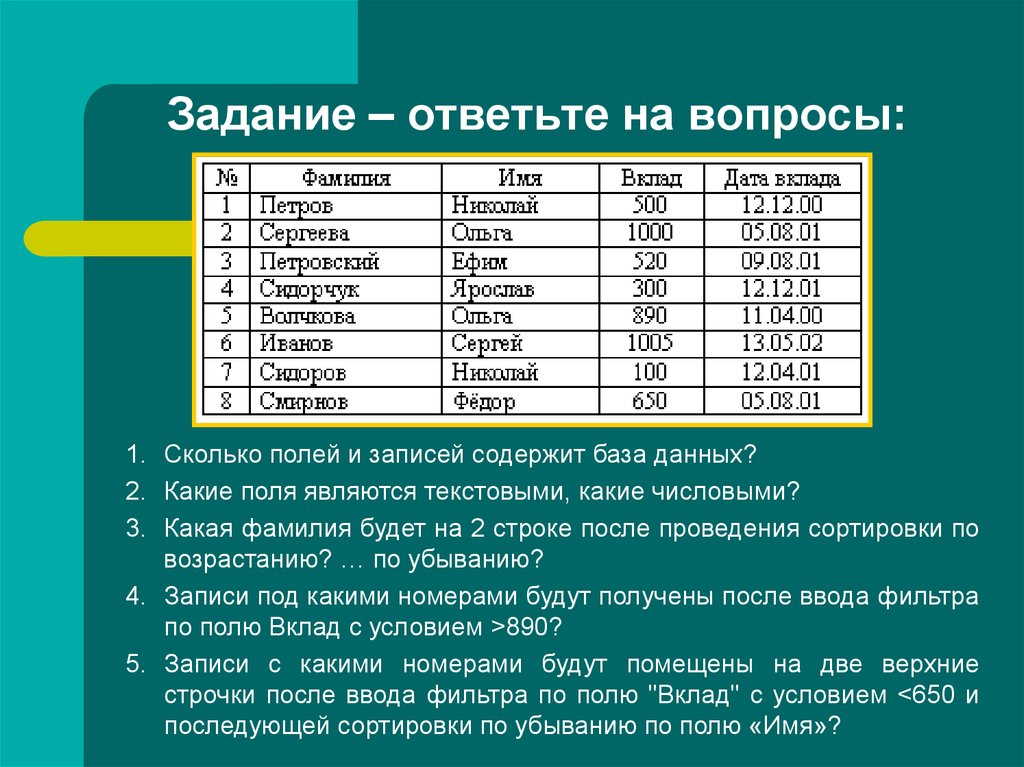

Будет ли чаще использоваться анализ во временной области или анализ в частотной области?

Анализ во временной области особенно полезен для схем с антеннами, где разработчик может столкнуться с паразитными сигналами, отражениями или сигналами отражения от земли. Обработка сигналов во временной области позволяет инженеру отделить посторонние сигналы во времени от полезного сигнала, тем самым идентифицируя искаженные сигналы.

В целом, использование частотной области математически упрощает анализ системы, в которой она работает. Многие известные инструменты SPICE будут в основном работать в частотной области из-за актуальности, эффективности и точности их аналитических функций.

Кроме того, математические системы являются важным классом систем, которые имеют различные практические применения. Кроме того, для математической системы, регулируемой линейными дифференциальными уравнениями, он переводит описание системы из временной области в частотную область. Таким образом, дифференциальное уравнение заменяется алгебраическим уравнением, которое значительно легче решить.

Взгляд на систему с точки зрения частоты часто дает врожденное понимание измеряемого качества, которое охватывает поведение системы. В настоящее время научное сообщество предлагает различную терминологию для описания такого характерного поведения физической системы применительно к изменяющимся во времени входным данным. Сюда входят такие термины, как частотная характеристика, полоса пропускания, фазовый сдвиг, усиление и резонансные частоты, и это лишь некоторые из них.

Одним из наиболее известных и универсальных примеров частотного содержания сигналов являются, пожалуй, аудиосигналы, такие как музыка. В этом случае анализ в частотной области дает лучшее понимание, чем анализ во временной области, потому что музыка неявно основана на разложении сложных звуков на отдельные составляющие частоты.

Осциллограф — бесценный инструмент для обнаружения сигналов.

Рассматривая синусоиду как звуковой сигнал, мы также должны учитывать изменения давления воздуха на наши уши как функцию времени. Таким образом, от теории работы музыкальных инструментов до нотной записи, используемой для записи и обсуждения самой музыки, требуется разделение частот компонентов для понимания рассматриваемого звука.

Анализ во временной области и анализ в частотной области являются бесценными инструментами анализа. Использование той или иной методологии зависит от ваших индивидуальных потребностей в дизайне. Однако во многих случаях именно использование обоих методов анализа дает наиболее полезную информацию о ваших потребностях в проектировании.

Независимо от того, требуется ли для вашей электроники анализ во временной или частотной области, с набором инструментов Cadence для проектирования и анализа вы обязательно будете оснащены. Однако до, во время и после анализа вам все равно понадобится инструмент компоновки, и Allegro может предоставить мощный механизм совместной работы для своего редактора компоновки.

Если вы хотите узнать больше о том, как у Cadence есть решение для вас, обратитесь к нам и нашей команде экспертов. Вы также можете посетить наш канал YouTube и посмотреть видеоролики о моделировании и системном анализе, а также ознакомиться с новинками нашего набора инструментов для проектирования и анализа.

Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.

Подпишитесь на LinkedIn

Посетите вебсайт

Больше контента от Cadence PCB Solutions

УЗНАТЬ БОЛЬШЕ

Представление сигналов во временной и частотной областях

Электрические сигналы имеют представление как во временной, так и в частотной областях. Во временной области напряжение или ток выражаются как функция времени, как показано на рисунке 1. Большинство людей относительно комфортно представляют сигналы во временной области. Сигналы, измеренные на осциллографе, отображаются во временной области, а цифровая информация часто передается в виде зависимости напряжения от времени.

Рис. 1. Представление электрического сигнала во временной области.

Сигналы также могут быть представлены величиной и фазой в зависимости от частоты. Сигналы, которые периодически повторяются во времени, представлены спектром мощности, как показано на рисунке 2. Сигналы, которые ограничены во времени (т. е. не равны нулю только в течение конечного времени), представлены энергетическим спектром, как показано на рисунке 3.

Рис. 2. Спектр мощности периодического сигнала.

Рис. 3. Энергетический спектр ограниченного во времени (переходного) сигнала.

Представления в частотной области особенно полезны при анализе линейных систем. Инженеры по электромагнитной совместимости и целостности сигналов должны уметь работать с сигналами, представленными как во временной, так и в частотной областях. Источники сигналов и помехи часто определяются во временной области. Однако поведение системы и преобразования сигналов более удобны и интуитивно понятны при работе в частотной области.

Линейные системы

Теория линейных систем играет ключевую роль в инженерном анализе электрических и механических систем. Инженеры моделируют множество вещей, включая поведение схемы, распространение сигнала, связь и излучение, как линейные преобразования. Поэтому важно точно определить, что мы подразумеваем под линейной системой, чтобы понять, как и когда использовать преимущества мощных инструментов анализа линейной системы, доступных нам.

На рис. 4 показана система с одним входом, x(t) и один выход, y(t)=H[x(t)] . Если ввод x ₁ (t) производит вывод y ₁ (t) , а ввод x ₂ (t) производит вывод y _{2 t 3 2 3 2 3 , то эта система является линейной тогда и только тогда, когда являются константами. Другими словами, масштабирование ввода с помощью константы даст результат, масштабированный с помощью той же константы; и объединение (суммирование) двух входов даст выход, который представляет собой сумму выходов, произведенных отдельными входами.}

Рисунок 4: Линейная система.

Контрольный вопрос

Какое из следующих уравнений описывает связь между выходом y(t) и входом x(t) линейной системы?

1. у=5x
2. у(т)=0
3. у=8х+3
4. у=х ²
5. у(т)=5т х(т)
6. у=sin x
7. y(t)=5 δ/δt [x(t)]

Из приведенных выше вариантов только a, b и g являются преобразованиями линейной системы. y=0 не очень интересная система, потому что ее выход всегда равен нулю, но она линейна. Простые производные и интегральные операторы являются линейными, поскольку они удовлетворяют условиям уравнения (1).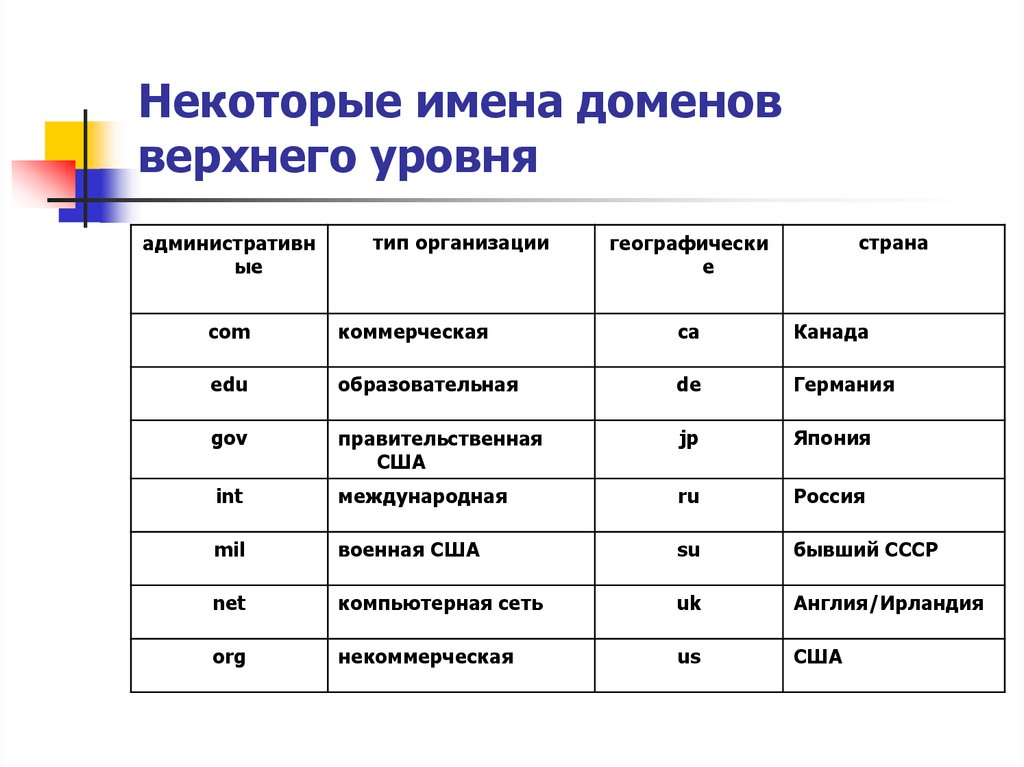 Остальные варианты не являются линейными операциями. Обратите внимание, что y=8x+3 — это уравнение прямой линии, но оно не описывает линейную систему, поскольку имеет ненулевой выход при отсутствии входных данных.

Анализ линейных систем в частотной области

Линейные системы обладают уникальным свойством: любой синусоидальный входной сигнал будет давать синусоидальный выходной сигнал с точно такой же частотой. Другими словами, если ввод имеет вид

x(t)=Aincos(ω0t+φin). (2)

, тогда выходные данные будут иметь вид

y(t)=Aoutcos(ω0t+φout). (3)

В общем случае амплитуда и фаза синусоидального сигнала могут изменяться, но частота должна быть постоянной. Это дает нам очень мощный инструмент для анализа линейных систем. Если мы представим входной сигнал как сумму его компонентов в частотной области, то мы можем выразить выход как простое масштабирование величин и сдвиг фаз этих компонентов.

Векторная запись

Для облегчения анализа откликов линейной системы на синусоидальные входные сигналы удобно представлять сигналы в сокращенной форме, известной как векторная запись. Рассмотрим ввод в форме

x(t)=Acos(ωt+φ). (4)

Это можно представить как

x(t)=Re{Aej(ωt+φ)}=A⋅Re{ejωtejφ}. (5)

, где Re{• } указывает действительную часть комплексной величины. Учитывая, что частота ω будет одинаковой во всей системе, нам не нужно специально записывать член e ^jωt , пока мы помним, что оно есть. То же самое относится к нотации Re{• } . Это позволяет нам выразить синусоидальный сигнал просто через его амплитуду и фазу как

x=Aejϕ или A∠ϕ. (6)

Выражение в (6) представляет собой сигнал в (4), выраженный с помощью векторной записи. Обратите внимание, что мы должны знать частоту сигнала, чтобы перейти от векторной записи к представлению во временной области.

Вопрос викторины

Запишите следующие сигналы, используя векторную запись:

1. x(t) = 5 cos(wt) вольт
2. y(t)=5 sin(wt) ампер
3. z(t) = 5t sin(wt) вольт

Первый сигнал, выраженный векторным представлением, представляет собой просто x = 5 вольт. Чтобы получить обозначение вектора для второго сигнала, мы признаем, что sin(ωt) = cos(ωt + π/2), поэтому y = 5e ^j(π/2) . Третий сигнал не является синусоидой и поэтому не может быть выражен с помощью векторной записи.

Ряд Фурье

Конечно, многие из входных сигналов линейных систем, которые мы хотели бы проанализировать, не являются синусоидальными. В этом случае желательно представлять более произвольные формы сигнала в виде суммы синусоидальных частотных составляющих. Затем мы анализируем каждый компонент по отдельности и применяем концепцию суперпозиции для восстановления выходного сигнала.

Периодический сигнал может быть представлен как сумма его частотных составляющих путем вычисления его коэффициентов ряда Фурье. Периодический сигнал с периодом T можно записать,

x(t)=∑n=−∞∞cnejn2πf0t (7a)

где

cn=1T∫t0t0+Tx(t)e−jn2πf0tdt. (7b)

Если x(t) является сигналом в области реального времени, коэффициенты c _n и c _-n являются комплексно-сопряженными (т.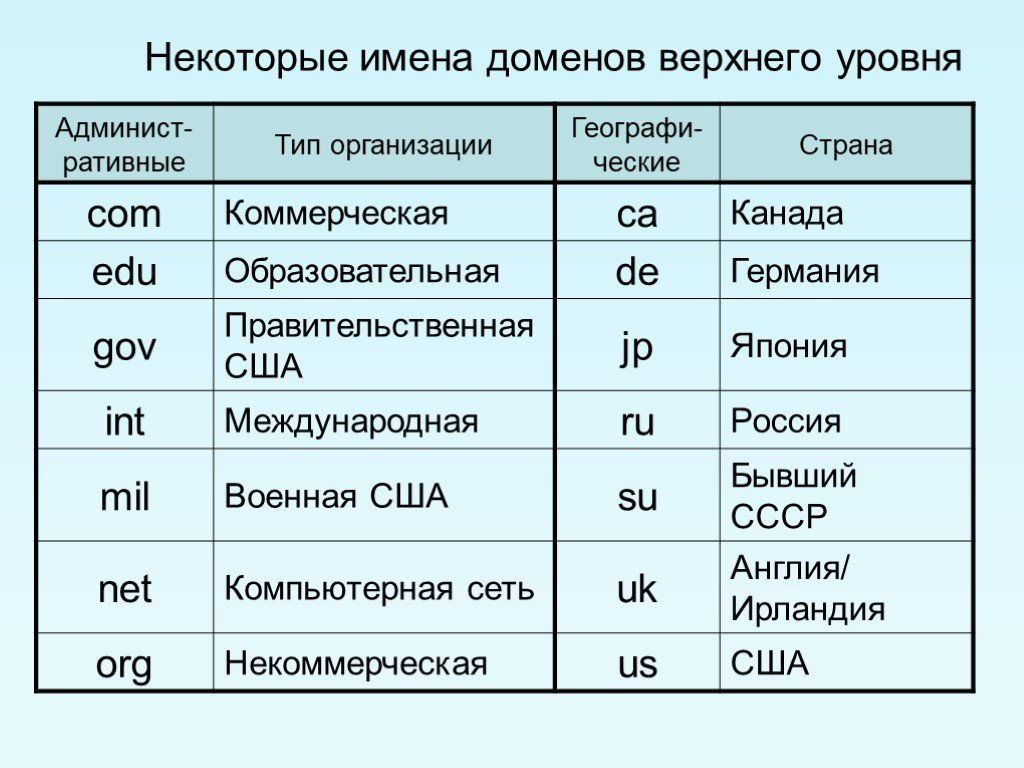 е. ), и мы можем переписать уравнение (7) в виде

x (t)=c0+∑n=1∞(cnejn2πf0t+cn∗e−jn2πf0t)=c0+∑n=1∞(|cn|ejn2πf0t+ϕn+|cn|e−(jn2πf0t+ϕn))=c0+∑n=1 ∞2|cn|cos(n2πf0t+ϕn). (8)

В этой форме мы видим, что коэффициенты ряда Фурье состоят из постоянной составляющей, c ₀ , и частоты положительных гармоник, nω ₀ (n = 1,2,3, …). Это односторонний ряд Фурье, и коэффициенты соответствуют амплитудам частотных гармоник, которые можно было бы измерить с помощью анализатора спектра.

Несколько периодических сигналов и их представления в частотной области показаны на рис. 5. Представление периодического сигнала в частотной области представляет собой линейчатый спектр. Он может иметь ненулевые значения только при постоянном токе, основной частоте и гармониках основной частоты. Поскольку у периодических сигналов нет ни начала, ни конца, ненулевые периодические сигналы имеют бесконечную энергию, но обычно имеют конечную мощность. Суммарная мощность сигнала во временной области,

Ptotal=1T∫t0t0+Tx2(t) dt.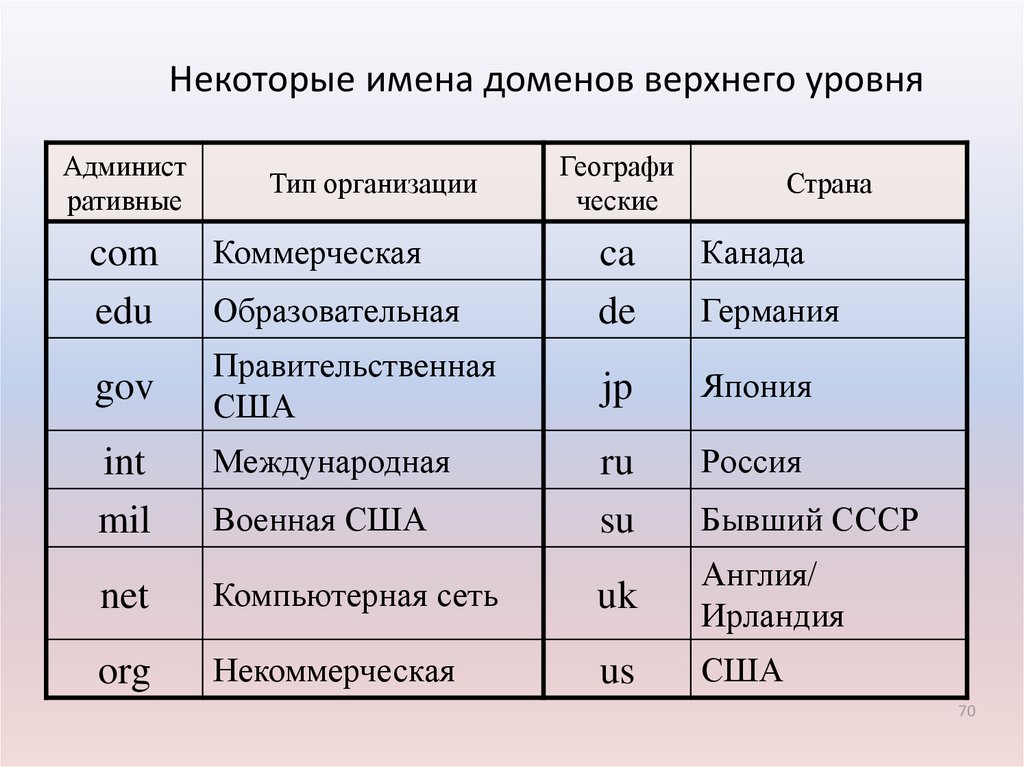 (9)

равно сумме мощностей в каждой компоненте частотной области,

Ptotal=∑n=−∞∞|cn|2. (10)

Рис. 5. Периодические сигналы во временной и частотной области.

Пример 1: Представление в частотной области последовательности импульсов

Определите представление в частотной области для последовательности импульсов, показанной на рис. 6.

Рис. 6: Последовательность импульсов.

Во временной области этот сигнал описывается следующей формулой:

x(t)={1 vnT

Коэффициенты ряда Фурье затем рассчитываются с использованием уравнения (7b) как −jn2πt/T dt=AτT[sin(nπτT)(nπτT)]e−j(nπτT). (E2)

Обратите внимание, что при τ→0 наш сигнал во временной области выглядит как последовательность импульсов, а амплитуды всех гармоник приближаются к одному и тому же значению. Когда τ→T/2, сигнал становится прямоугольным, а величина гармоники становится равной

cn=A2|sin(nπ2)(nπ2)||e−j(nπ2)|={Anπn=±1,±3,±5⋯0n=±2,±4,±6⋯. (E3)

В этом случае амплитуда четных гармоник равна нулю, а нечетные гармоники линейно уменьшаются с частотой (n).

Преобразование Фурье

Переходные сигналы (то есть сигналы, которые начинаются и заканчиваются в определенное время) также могут быть представлены в частотной области с помощью преобразования Фурье. Представление преобразования Фурье переходного сигнала x(t) задается следующим образом:

X(f)=∫−∞∞x(t) e−j2πf​tdt. (11)

Обратное преобразование Фурье можно использовать для преобразования представления сигнала в частотной области обратно во временную область,

x(t)=12π∫−∞∞X(f) ej2πf​tdf. (12)

Некоторые переходные сигналы во временной области и их преобразование Фурье показаны на рисунке 7.

Рисунок 7. Переходные сигналы во временной и частотной области.

Обратите внимание, что переходные сигналы имеют нулевую среднюю мощность (при усреднении за все время), но имеют конечную энергию. Полная энергия в переходном сигнале во временной области определяется выражением

E=∫−∞∞x2(t) dt. (13)

Это должно равняться полной энергии в представлении сигнала в частотной области,

E=∫−∞∞|X(f)|2 df. (14)

Представление трапециевидного сигнала в частотной области

Давайте рассмотрим представление в частотной области периодического трапециевидного сигнала, показанного на рис. в общем. Кроме того, сходство между трапециевидной формой волны и обычными формами цифровых сигналов будет полезно, когда мы исследуем проблемы электромагнитной совместимости или целостности сигнала в цифровых системах.

Рис. 8. Трапециевидный сигнал.

Используя односторонний ряд Фурье, уравнения (7b) и (8), мы можем представить этот сигнал как сумму его частотных составляющих [1],

x(t)=c0+∑n=1∞2 |cn|cos(n​​2πf0​t+ϕn). (15)

, где

2|cn|=2AτT|sin(nπτT)(nπτT)||sin(nπtrT)(nπtrT)|. (16)

Уравнение (16) можно вывести, заметив, что трапецеидальная форма волны на рисунке 7 может быть получена путем свертки последовательности импульсов на рисунке 9. с другой последовательностью импульсов, импульсы которой имеют ширину t _r и амплитуду A/t _r . Свертка во временной области эквивалентна умножению в частотной области, поэтому мы можем просто перемножить два представления этих последовательностей импульсов в частотной области, чтобы получить уравнение (16).

Каждый член, 2| c _n |, — амплитуда n-й гармоники. Если предположить, что t _r < Это частотное представление трапециевидного сигнала (τ=T2, tr≪T) и его огибающая показаны на рисунке 9..

Рисунок 9: Представление трапециевидного сигнала в частотной области

Пример 2: Гармоники трапециевидного сигнала

Форма волны, показанная на рисунке 10 ниже, измерена на осциллографе в лаборатории. Время нарастания и спада составляет 0,8 нс.

а.) Что такое основная частота?

b.) Рассчитайте амплитуды гармоник на частотах 50 МГц, 150 МГц, 250 МГц и 1,55 ГГц.

Если время нарастания и спада увеличить до 1,6 нс, то на сколько дБ уменьшится гармоника на частотах 50, 150, 250 и 550 МГц? 9Рисунок 10. Трапециевидная форма волны для примера 2 Поэтому нас просят определить амплитуды гармоник 1 , 3 , 5 и 11 . Применяя уравнение (16) для n = 1,3,5 и 11, получаем амплитуды этих гармоник:

2|c1|=2(1 v)2|sin(1π(10)20)(1π(10) 20)||sin(1π(0,8)20)(1π(0,8)20)|=(1 v)(0,64)(1,00)=0,64 v2|c3|=2(1 v)2|sin(3π(10) )20)(3π(10)20)||sin(3π(0,8)20)(3π(0,8)20)|=(1 v)(0,21)(0,98)=0,21 v2|c5|=2(1 v)2|sin(5π(10)20)(5π(10)20)||sin(5π(0,8)20)(5π(0,8)20)|= (1 v)(0,13)(0,94)=0,12 v2|c11|=2(1 v)2|sin(11π(10)20)(11π(10)20)||sin(11π(0,8)20)( 11π(0,8)20)|=(1 v)(0,06)(0,71)=0,04 v

Ни на одну из этих гармоник существенно не влияет время нарастания. Они имеют практически ту же амплитуду, что и при нулевом времени нарастания. Однако увеличение времени нарастания до 1,6 нс существенно влияет на амплитуду верхних гармоник:

2|c1|=2(1 v)2|sin(1π(10)20)(1π(10)20)||sin( 1π(1,6)20)(1π(1,6)20)|=(1 v)(0,64)(0,99)=0,63 v2|c3|=2(1 v)2|sin(3π(10)20)(3π(10)20)||sin(3π(1,6)20)(3π(1,6)20)|= (1 v)(0,21)(0,91)=0,19 v2|c5|=2(1 v)2|sin(5π(10)20)(5π(10)20)||sin(5π(1,6)20)( 5π(1,6)20)|=(1 v)(0,13)(0,76)=0,10 v2|c11|=2(1 v)2|sin(11π(10)20)(11π(10)20)||sin (11π(1,6)20)(11π(1,6)20)|=(1 v)(0,06)(0,13)=0,008 v.

Удвоение времени нарастания с 0,8 до 1,6 нс уменьшает первую гармонику всего на 20log(0,64,63) )=0,14 дБ. Третья гармоника уменьшается на 20 log (0,21,19) = 0,87 дБ. Пятая гармоника уменьшается на 20 log (0,12,10) = 1,6 дБ, а одиннадцатая гармоника уменьшается на 20 log (0,040,008) = 14 дБ.

Обратите внимание, что изменение времени нарастания может оказать существенное влияние на амплитуду верхних гармоник без существенного изменения представления сигнала во временной области.

This entry was posted in Популярное