Окружность, круг, сегмент, сектор. Формулы и свойства

• Окружность — определение
• Круг — определение
• Радиус и диаметр окружности
• Основные свойства окружности
• Формулы длины окружности и площади круга
• Уравнение окружности
• Касательная окружности и ее свойства
• Секущая окружности и ее свойства
• Хорда окружности и ее свойства
• Центральный угол, вписанный угол и их свойства
• Дуга, длина дуги, градусная мера дуги
• Полуокружность и полукруг
• Сектор, площадь сектора
• Сегмент, площадь сегмента
• Концентрические окружности
• Кольцо

Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.

Определение. Единичная окружность — окружность, радиус которой равен единице.

Определение. Круг — часть плоскости, ограничена окружностью.

Определение. Радиус окружности R — расстояние от центра окружности О до любой точки окружности.

Определение. Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.

Основные свойства окружности

1. Диаметр окружности равен двум радиусам.

D = 2r

2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.

3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.

4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.

5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.

Формулы длины окружности и площади круга

Формулы длины окружности

1. Формула длины окружности через диаметр:

L = πD

2. Формула длины окружности через радиус:

L = 2πr

Формулы площади круга

1. Формула площади круга через радиус:

S = πr²

2. Формула площади круга через диаметр:

S = πD²4

Уравнение окружности

1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:

r² = x² + y²

2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

r² = (x — a)² + (y — b)²

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

Касательная окружности и ее свойства

Определение. Касательная окружности — прямая, которая касается окружности только в одной точке.

Основные свойства касательных к окружности

1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.

2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

AB = AC

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

∠ОAС = ∠OAB

Секущая окружности и ее свойства

Определение. Секущая окружности — прямая, которая проходит через две точки окружности.

Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:

AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:

AQ ∙ BQ = CQ²

Хорда окружности ее длина и свойства

Определение. Хорда окружности — отрезок, который соединяет две точки окружности.

Длина хорды

1. Длина хорды через центральный угол и радиус:

AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:

AB = 2r sin α

Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:

если хорды AB = CD, то

дуги ◡ AB = ◡ CD

2. Если хорды параллельные, то дуги между ними будут одинаковые:

если хорды AB ∣∣ CD, то

◡ AD = ◡ BC

3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:

если OD ┴ AB, то

AC = BC

4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:

AQ ∙ BQ = DQ ∙ QC

5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.

если хорды AB = CD, то

ON = OK

6. Чем больше хорда, тем ближе она к центру.

если CD > AB, то

ON < OK

Центральный угол, вписанный угол и их свойства

Определение. Центральный угол окружности — угол, вершиной которого есть центр окружности.

Определение. Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.

Основные свойства углов

1. Все вписанные углы, которые опираются на одну дугу — равны.

2. Вписанный угол, который опирается на диаметр будет прямым (90°).

3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу

β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.

α + β = 180°

Определение. Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.

Определение. Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.

Формула длины дуги через центральный угол (в градусах):

l = πr180°∙ α

Определение. Полуокружность — дуга в которой концы соединены диаметром окружности.

Определение. Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.

Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)

S = πr²360°∙ α

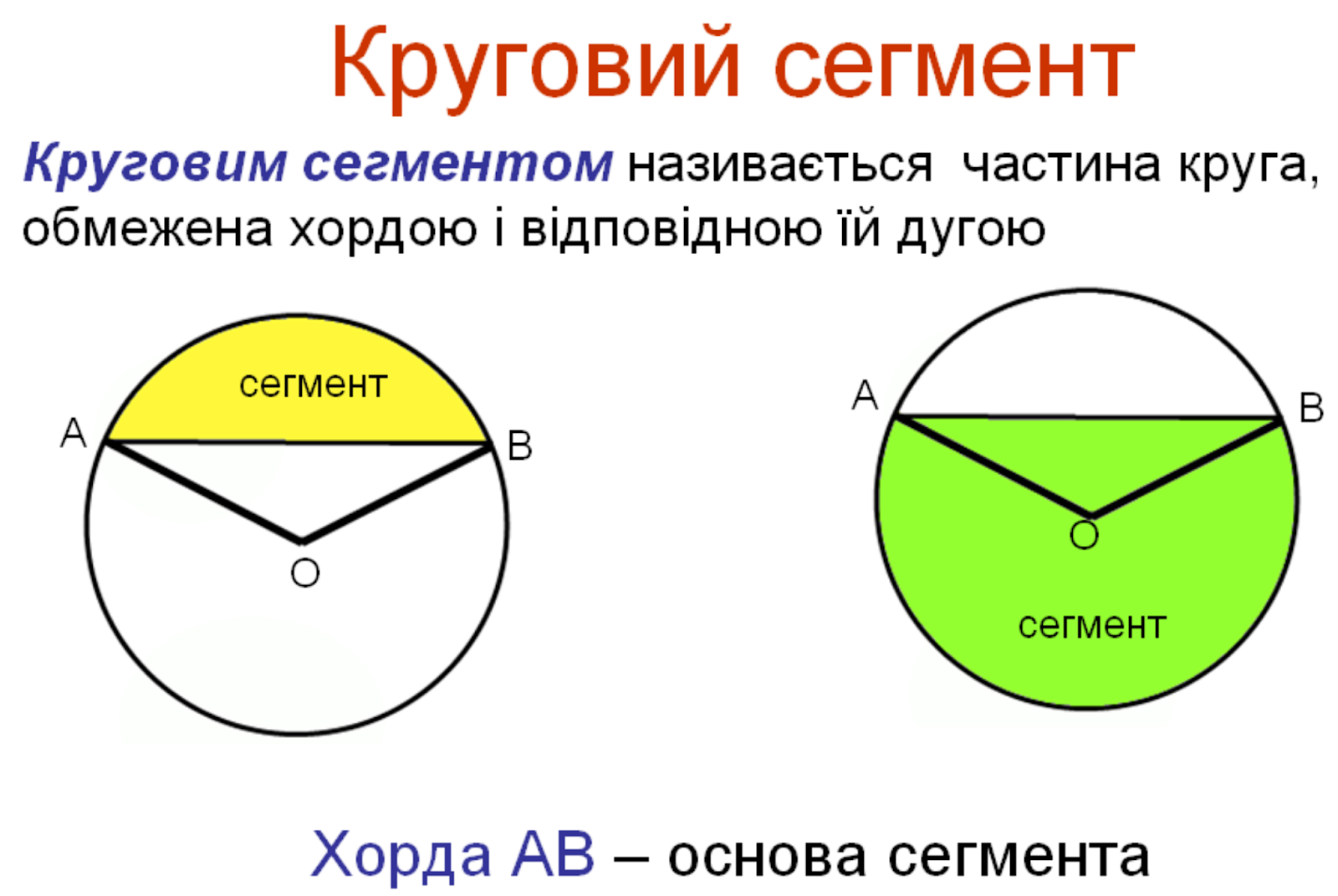
Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.

Определение. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.

Определение. Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.

Все таблицы и формулы

Отрасль и сектор, в чем разница? — Тюлягин

Тюлягин > Инвестиции > Фундаментальный анализ > Анализ секторов и отраслей > Вы здесь и сейчас

Здравствуйте, уважаемые читатели проекта Тюлягин! Хотя многим читателям, эти два понятия могут показаться одинаковыми, термины «отрасль» (отрасль промышленности/индустрия) и «сектор» имеют немного разные значения. Отрасль (индустрия) относится к гораздо более конкретной группе компаний или предприятий, в то время как термин сектор описывает большой сегмент экономики.

Содержание статьи:

• Отрасль и сектор: обзор
• Отрасль (индустрия) — что это такое
• Сектор — что это такое
• Прочие особенности
• Резюме

Отрасль и сектор: обзор

Термины «отрасль» и «сектор» часто используются как синонимы для описания группы компаний, которые работают в одном и том же сегменте экономики или имеют схожий тип бизнеса. Термин «сектор» часто относится к более крупной, общей части экономики, в то время как слово «отрасль» имеет гораздо более конкретное значение.

Эти два термина иногда меняют местами. Но общая идея остается: один разбивает экономику на несколько общих сегментов, в то время как другой далее классифицирует их по более конкретным видам деятельности. На фондовом рынке общепринятая терминология называет сектор широкой классификацией, а индустрия (отрасль/отрасль промышленности) — более конкретной.

Отрасль (индустрия) — что это такое

Отрасль относится к определенной группе компаний, которые работают в аналогичной сфере бизнеса. По сути, индустрии создаются путем разделения секторов на более определенные группы. Поэтому эти компании делятся на более конкретные группы, чем секторы. В каждом из дюжины или около того секторов будет различное количество отраслей, но их могут быть сотни.

Финансовый сектор может быть разбит на несколько различных индустрий, таких как банки, компании по управлению активами, страхованию жизни, или брокерские компании. Компании, относящиеся к одной индустрии, конкурируют за клиентов, предлагая аналогичные услуги. Например, банки будут конкурировать друг с другом за клиентов, открывающих текущие и сберегательные счета, в то время как компании по управлению активами ищут инвестиционных клиентов.

Но это не все. Эти индустрии можно разделить на более конкретные группы. Например, индустрия страхования может быть разбита на различные специализированные подразделения, такие как страхование жилья, автомобиля, жизни и корпоративное страхование.

При выборе инвестиционной возможности инвестору может быть проще сравнить разные компании в одной индустрии (отрасли). Это потому, что они могут использовать одни и те же производственные процессы, обслуживать одну и ту же клиентскую базу или иметь схожую финансовую отчетность.

Акции компаний одной отрасли (индустрии) обычно торгуются в одном направлении. Это потому, что компании в одной отрасли подвержены влиянию одних и тех же (или похожих) факторов.

Сектор — что это такое

Сектор — это один из немногих общих сегментов экономики, в которые можно отнести большую группу компаний. Экономику можно разбить примерно на дюжину секторов, которые могут описывать почти всю деловую активность в этой экономике. Экономисты могут проводить более глубокий анализ экономики, рассматривая каждый отдельный сектор.

В экономике есть четыре различных сектора:

• Первичный сектор: этот сектор занимается добычей и сбором природных ресурсов, таких как сельское хозяйство и горнодобывающая промышленность.
• Вторичный сектор: этот сектор включает строительство, производство и переработку. В основном в этот сектор входят отрасли, связанные с производством готовой продукции из сырья.
• Третичный сектор: розничные торговцы, развлекательные и финансовые компании составляют этот сектор. Эти компании предоставляют услуги потребителям.
• Четвертичный сектор: последний сектор занимается знаниями или интеллектуальными занятиями, включая исследования и разработки (НИОКР), бизнес, консалтинговые услуги и образование.

Например, сектор основных материалов экономики включает компании, которые занимаются разведкой, обработкой и продажей основных материалов, таких как золото, серебро или алюминий. Эти материалы используются в других секторах экономики. В секторах часто есть определенные биржевые фонды (ETF), которые отслеживают сектор, например, Фонд SPDR Energy Select Sector. Транспорт — еще одна отрасль экономики. Этот сектор включает автомобилестроение, производство поездов, грузовиков и авиаперевозок.

Инвесторы могут использовать секторы как способ классифицировать акции, в которые они инвестируют, такие как телекоммуникации, транспорт, здравоохранение и финансы. Каждый сектор имеет свои особенности и риски.

Прочие особенности

При оценке компаний разумнее всего оценивать компании внутри отрасли, а не компании внутри сектора. Это так, потому что, как отмечалось выше, каждый сектор можно разделить на разные отрасли. Например, сектор авиаперевозок будет включать компании, которые строят самолеты, такие как Boeing и Airbus, авиакомпании, которые фактически эксплуатируют самолеты и перевозят клиентов из одного пункта назначения в другой, пищевые компании, которые сосредоточены на обеспечении бортовым питанием, и так далее.

Хотя все эти компании работают в секторе авиаперевозок и пострадают, если в целом сектор улучшится или понесет убытки, у них совершенно разные капитальные затраты, денежные потоки, операционная маржа и так далее. Следовательно, при использовании финансовых коэффициентов для сравнения одной компании с другой, она должна быть из той же отрасли, например, сравнивать Boeing и Airbus, а не сравнивать Boeing с бортовым поставщиком питания, чтобы обеспечить «сравнение яблок с яблоками».

Резюме

• Термин «индустрия» относится к группе компаний, работающих в схожей сфере бизнеса, и его категоризация более узкая.
• Сектор относится к той части экономики, в которой большое количество компаний может быть отнесено к категории и которая больше по сравнению с ними.
• Инвесторы могут легко сравнить компании в одной отрасли по инвестиционным возможностям.
• Акции компаний, работающих в одной отрасли, обычно торгуются в одном направлении, поскольку на их фундаментальные показатели одинаково влияют рыночные факторы.
• В экономике четыре различных сектора: первичный, вторичный, третичный и четвертичный.

А на этом сегодня все про отрасль и сектор. Надеюсь статья оказалась для вас полезной. Делитесь статьей в социальных сетях и мессенджерах и добавляйте сайт в закладки. Успехов и до новых встреч на страницах проекта Тюлягин!

Площади сектора и сегмента круга: Формулы, Теорема

• Автор
  Сушма_П
• Последнее изменение 24-01-2023

Площадь сектора круга — это площадь, охватываемая границами сектора. Сектор всегда выходит из центра круга. Полукруг также является сектором круга. Дуга и хорда окружности ограничивают площади сектора и сегмента окружности.

Когда мы делим что-то на части, каждая часть называется сегментом. Это определенная часть, разделенная хордой окружности. Давайте узнаем больше о площади сектора и площади сегмента круга.

Сектор круга определяется как часть круга, ограниченная двумя радиусами и дугой, соединяющей их. Пространство, занимаемое сектором круга, называется площадью сектора круга.

Существует два типа секторов: основной сектор и второстепенный сектор. Большой сектор — это сектор, который больше полукруга, тогда как второстепенный сектор — это сектор, который меньше полукруга. На рисунке ниже представлены сектора в круге. Заштрихованная часть \(O A P B\) — это площадь малого сектора, а незаштрихованная часть \(O A Q B\) — площадь большого сектора круга.

Пример:

Одним из наиболее распространенных реальных примеров площади сектора является кусок пиццы. Форма кусочков пиццы похожа на сектор круга. Пицца радиусом \(7\) дюймов разделена на 6 ломтиков одинакового размера, как показано на рисунке ниже. Каждый срез представляет собой сектор.

Площадь сектора формулы круга

Площадь сектора формулы круга можно рассчитать, чтобы найти общее пространство, покрытое частью круга. Площадь сектора может быть рассчитана двумя различными способами в зависимости от заданной единицы измерения угла.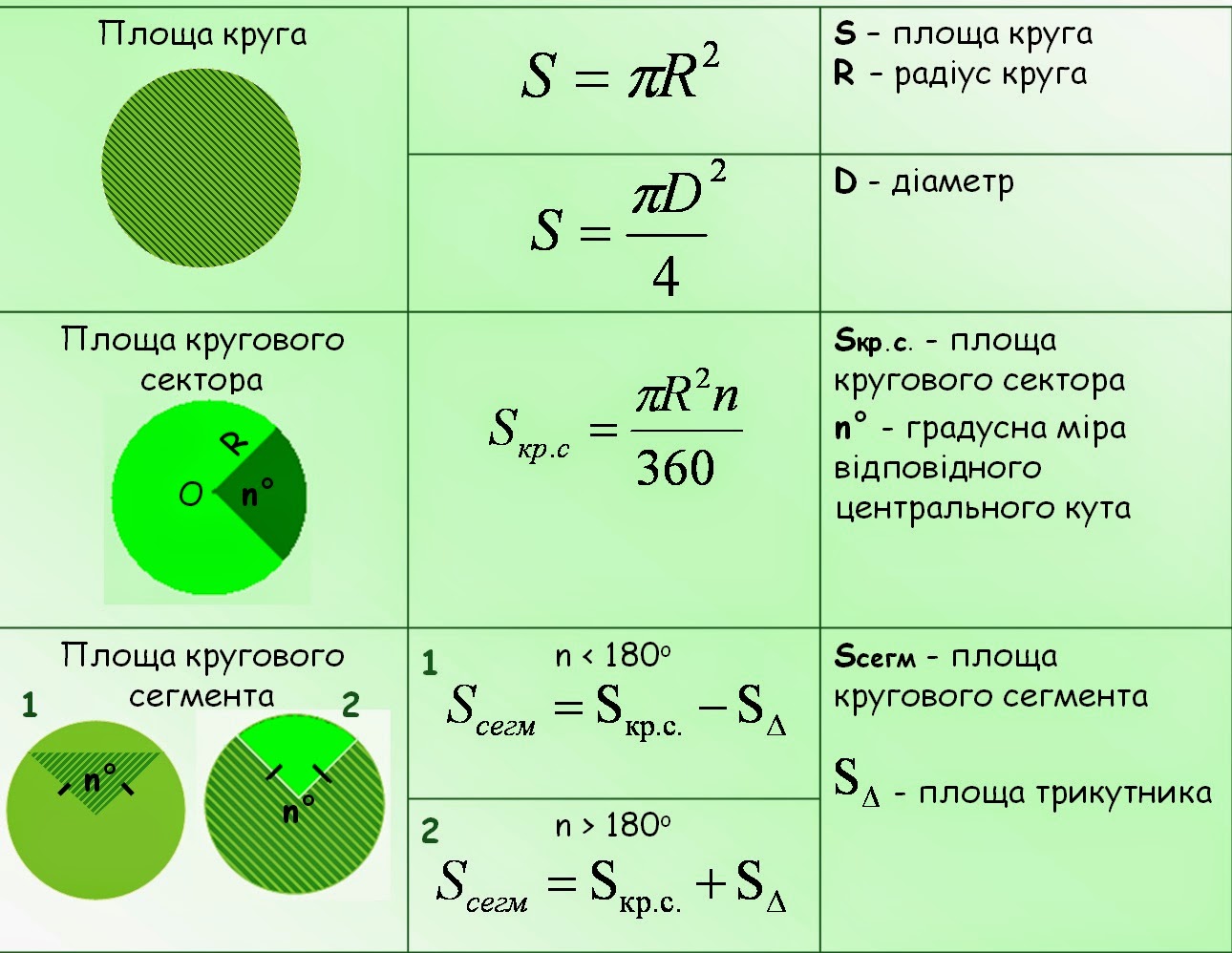 Ниже приведены формулы для вычисления площади сектора круга: 9{2} \theta\), где \(r\) — радиус окружности, а \(\theta\) (в радианах) — угол, стягиваемый в центре.

Сегмент окружности Определение

Сегмент окружности — это площадь, покрываемая хордой и дугой окружности. Определим хорду и дугу окружности.

1. Хорда – это отрезок, соединяющий любые две точки на окружности окружности.
2. Дуга — это часть периметра (окружности) круга.

Существует два типа сегментов. Большой сегмент и второстепенный сегмент. Большой отрезок образует большая дуга, а меньшая дуга образует меньший отрезок окружности.

Площадь сегмента окружности

На приведенном ниже рисунке дуга \(P Q\) и два радиуса \((O P\) и \(O Q)\) окружности образуют сектор. Эти два радиуса вместе с хордой отрезка образуют треугольник \(P O Q\). Таким образом, площадь сегмента круга можно получить, вычитая площадь треугольника \(P O Q\) из площади сектора \(P O Q\). {2} \sin \theta\). 92}}}{2}} \right)\left[ {\theta – \sin \,\theta } \right],\) когда \(\theta\) задано в радианах

Теоремы об отрезке Круг

В основном, есть две теоремы, основанные на сегменте круга.

1. Теорема об углах в одном и том же сегменте
2. Теорема об альтернативных сегментах

Углы в одном и том же сегменте Теорема

Утверждает, что углы , образованные в одном и том же сегменте окружности, всегда равны.

Альтернативный сегмент Теорема 9{2}=\frac{11 \times 7}{2}=38,5 \mathrm{кв.см}\).

Следовательно, площадь малого сектора равна \(38,5 \mathrm{sq} \cdot \mathrm{см}\).

Q.2. Значок в форме круга разделен на \(6\) секторов проводами \(3\) . Длина диаметра \(2\) ед. Вычислите площадь каждого сектора значка?
Ответ: Учитывая, диаметр значка \(d\) составляет \(2\) единиц. 9{\circ}} \times \frac{22}{7} \times 1=\frac{11}{21}\) sq.units
Следовательно, площадь каждого сектора значка равна \(\frac{11 {21}\) квадратных единиц.

Q.3. Зонт имеет \(10\) ребер, расположенных на равном расстоянии друг от друга, если рассматривать его как плоский круг радиусом \(7\) единиц. Вычислите площадь между двумя последовательными ребрами зонта.
Ответ: Радиус плоского зонта \(=7 \,\text {единиц}\) 9{2}=15,4 \mathrm{кв.ед.}\).
Следовательно, площадь между двумя соседними ребрами зонта равна \(15,4 \,\text {кв.ед.}\).

Q.4. Если площадь сектора равна \(80 \,\text {кв.см}\)  , а площадь заключенного треугольника равна \(68 \,\text {кв.см}\ ) , вычислить площадь сегмента?
Ответ: Используя соотношение, площадь сегмента \(=\) площадь сектора \(-\) площадь треугольника
\(=(80-68) \,\mathrm{кв.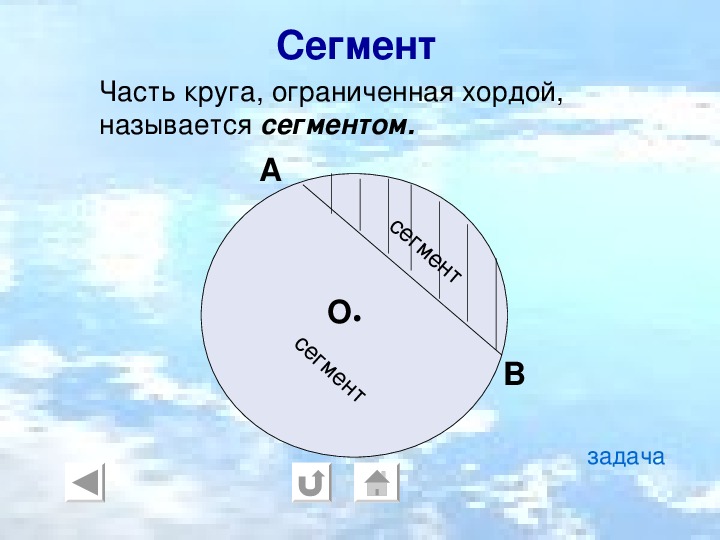 } . \mathrm{см}\)
\(=12 \,\mathrm{кв.см}\)
Таким образом, площадь отрезка равна \ (12 \,\mathrm{кв.см}\).

Q.5. Вычислить площадь большого сегмента круга, если площадь его меньшего сегмента равна \(54 \,\text {кв. ед.}\) , а радиус равен \(7 \,\text { ед.}\) . Используйте  \(\pi=\frac{22}{7}\) .
Ответ: Используя соотношение, площадь большого сегмента \(=\) площадь круга \(-\) площадь меньшего сегмента 9{2}-54\)
\(=\frac{22}{7} \times 7 \times 7-62\)
\(=92 \,\text {кв.ед.}\)
Следовательно, площадь основного сегмента составляет \(92 \,\mathrm{кв. единиц}\)

Резюме 

Эта статья включает две важные темы: площадь сектора круга и площадь сегмента круга. Мы узнали определения обоих. Затем мы изучали большие и малые сектора круга, а также большие и малые сегменты круга.

Далее мы изучили формулы для вычисления площади сектора круга и площади сегмента круга.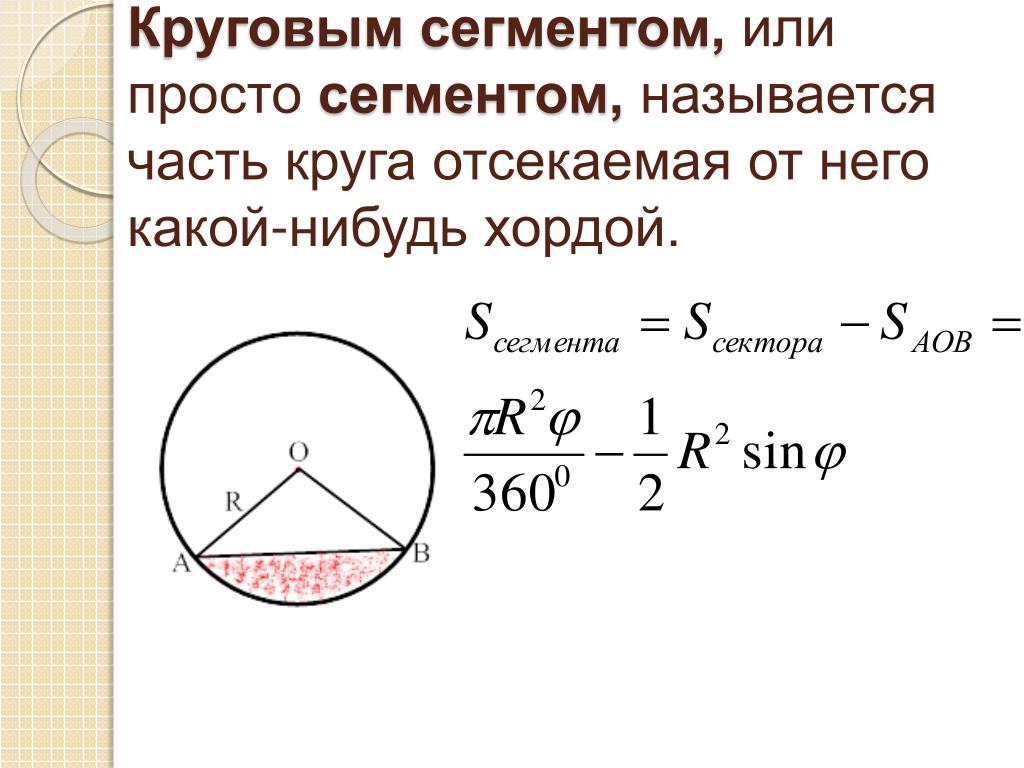 Наконец, мы кратко обсудили теоремы, основанные на сегменте окружности. 9{2}\)

Q.3. Какие действия нужно выполнить, чтобы найти площадь сегмента круга?
Ответ: Шаги для нахождения площади сегмента круга:
(i) По заданному радиусу круга и величине центрального угла, занимаемого дугой, определить площадь сектора круга. круг.
(ii) Найдите площадь треугольника, образованного двумя радиусами и хордой отрезка.
(iii) Вычтите площадь треугольника из площади сектора, чтобы получить площадь сегмента.

Q.4. Чем отличается сегмент круга от сектора круга?
Ответ: Сегмент окружности — это область, ограниченная хордой и соответствующей ей дугой, а сектором окружности является область, ограниченная двумя радиусами и соответствующей дугой.

Q.5. Как площадь сектора связана с площадью круга?
Ответ: Если угол в центре круга равен \(1^{\circ}\), площадь сектора равна \(\frac{\pi r^{2}}{ 360^{\circ}}\). {2}\), где \(r\) — радиус окружности, а \(\theta\) — угол, стягиваемый в центре, в градусах.

В чем разница между сектором и сегментом круга

• Популярные категории
• Структура данных
• Сеть
• РСУБД
• Операционная система
• Ява
• MS Excel
• iOS
• HTML
• УСБ
• Андроид
• Питон
• Программирование на С
• С++
• С#
• МонгоДБ
• MySQL
• Javascript
• PHP
• Физика
• Химия
• Биология
• Математика
• Английский
• Экономика
• Психология
• Социальные науки
• Модные исследования
• Юридические исследования

• Выбранное чтение
• Примечания к экзаменам UPSC IAS
• Передовой опыт разработчиков
• Вопросы и ответы
• Эффективное составление резюме
• HR Вопросы на собеседовании
• Компьютерный глоссарий
• Кто есть кто

Решение:

• Дуга AB образует угол с центром окружности O.
  

  This entry was posted in Популярное