Как распределять деньги правильно для развития бизнеса и роста прибыли

Для наглядности покажем теорию на примере Максима. Он — ИП на УСН «Доходы». Месяц назад взял кредит, арендовал отдел в торговом центре и открыл цветочный магазин. Работников нет, всё делает сам. 

Погасите расходы за текущий месяц и отложите запас на следующий

Даже если вы знаете, что у вас есть выручка, не стоит сразу забирать её себе или полностью пускать на продвижение. Сначала нужно убедиться, что бизнесу хватит денег на оплату расходов в этом месяце и работу в следующем.

Суммируйте все основные затраты на бизнес: 

• на аренду помещения;
• коммунальные услуги;
• зарплату сотрудникам;
• материалы;
• кредиты;
• налоги. 

Теперь вы видите, сколько денег нужно, чтобы покрыть расходы на текущий месяц. В идеале эту сумму нужно сразу отложить и на следующий. 

Выручка цветочного магазина за первый месяц составила 410 000 ₽. Максим подсчитал, что за это время на бизнес ушло 276 000 ₽: 80 000 ₽ на аренду, 7 000 ₽ на коммунальные услуги, 150 000 ₽ на покупку цветов и расходных материалов, 30 000 ₽ на оплату кредита и 9 000 ₽ на налоги. Эти расходы удалось покрыть за счёт кредита, но 276 000 ₽ Максим заранее отложил на второй месяц работы. 

Подсчитайте, какую прибыль принёс бизнес за месяц

Если вы знаете сумму всех расходов, то сможете подсчитать прибыль бизнеса. Для этого нужно вычесть из выручки все траты. Оставшуюся сумму можно распределять без страха застопорить рабочий процесс из-за нехватки средств.

После того как Максим отложил деньги на следующий месяц, у него осталось 410 000 ₽ − 276 000 ₽ = 134 000 ₽. Эта сумма — прибыль цветочного магазина за первый месяц. 

Разделите прибыль между вкладом в бизнес, запасом на чёрный день и своими доходами 

Примерная схема распределения прибыли выглядит так:

40 % — в развитие бизнеса. Например, на рекламу, запуск новых продуктов, курсы повышения квалификации. 

Если не вкладываться в развитие бизнеса, со временем он может рухнуть. Покупатели перейдут к конкурентам, которые регулярно совершенствуют навыки и обновляют ассортимент.

20 % — в резервный фонд. Это запас на случай форс-мажора. Например, если сломается оборудование или подведёт поставщик, резервный фонд поможет избежать кассового разрыва и не влезть в долги. 

Эту часть прибыли лучше хранить на отдельном счёте или откладывать на депозит. Но важно, чтобы вы в любой момент могли снять деньги. 

40 % — в дивиденды. Это ваш собственный доход. Если не планировать выплаты себе, вся прибыль может незаметно уйти в дело, а вы останетесь ни с чем.

У каждого бизнеса свои цели и потребности, поэтому проценты выше — ориентировочные. Если вы только запускаетесь, большая часть прибыли может уходить на развитие и продвижение. Если у бизнеса уже есть подушка безопасности, половину вложений в резервный фонд можно перекинуть в собственные дивиденды.

Максим хочет, чтобы о нём узнало как можно больше потенциальных клиентов, поэтому половину первой прибыли — 67 000 ₽ — потратил на продвижение. Запустил таргетированную рекламу, чтобы раскрутить профиль магазина во ВКонтакте, а также подключил Рекламную подписку от Яндекс Бизнеса, чтобы привлекать клиентов с площадок Яндекса и Google.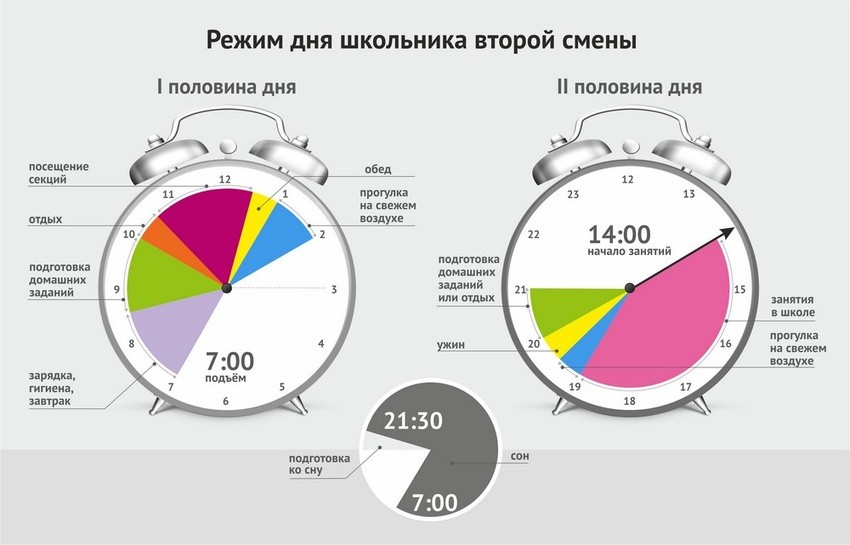 26 800 ₽ (20 % прибыли) Максим отложил на чёрный день и остаток 40 200 ₽ забрал себе в кошелёк.

Было полезно? Хотите что-то добавить или спросить? 
Присоединяйтесь к обсуждению во ВКонтакте или Телеграме.

Поделиться:

рассылка для бизнеса раз в две недели

Как распределить время на ЕГЭ по математике

Автор статьи Анна Малкова.
Эта статья не заменит подготовки к ЕГЭ на курсах ЕГЭ или с репетитором. Зато вы узнаете, как правильно распределить время на профильном ЕГЭ по математике, чтобы получить максимальные баллы.

Вы, конечно, видели в сборниках для подготовки к ЕГЭ рекомендации начинать с самых простых задач, а потом переходить к сложным. И если задача не получилась, то пропускать ее и переходить к следующей. Раньше такая рекомендация была и в демоверсии профильного ЕГЭ по математике. Сейчас ее убрали. Почему?

Если вы пришли на ЕГЭ, вообще ничего не зная, то да, вам надо выбрать из варианта самые простые задачи, где вы хоть что-то сможете сделать. Но тогда лучше сразу выбрать базовый ЕГЭ по математике и не мучиться.

А если вы хотите сдать профильную математику на 100 баллов? Или хотя бы на 80-90?

Запомним: если вы идете на высокий балл, первые 12 заданий профильного ЕГЭ по математике вам надо решать за полчаса. Правильно и без ошибок. И успеть перенести ответы в бланк ЕГЭ. Достигается это только тренировкой.

Ответы проверяем и переносим в бланк ЕГЭ сразу, чтобы не возвращаться к ним 100 раз.

И после того, как 12 задач с кратким ответом решены, – переходим к сложным задачам профильного ЕГЭ по математике. А это задачи с 13 по 19.

Здесь важна стратегия. Если вы весь 11 класс (а лучше еще и десятый) занимались на курсах ЕГЭ или с репетитором, вы легко решите еще три задачи:

№ 13 – уравнение;
№15 – неравенство;
№17 — экономическую.

Это алгебра. Получается у всех. Если до ЕГЭ 2 месяца, вы хотите сдать профильный ЕГЭ по математике на высокий балл, но не решаете эти задачи – срочно на курсы экспресс-подготовки к ЕГЭ! Потому что у репетиторов за 2 месяца до ЕГЭ вряд ли будет для вас свободное время.

На решение этих трех задач по алгебре – час. За это время надо успеть и решить их, и проверить (например, подставить найденные корни в уравнение), и оформить решение на чистовике.

Теперь у вас есть около двух с половиной часов и 4 сложных задачи. И если вы уже решили правильно все предыдущие, вы набрали около 70-75 баллов. Отлично! Теперь самое интересное!

Смотрим на 4 сложных задачи профильного ЕГЭ по математике.

Это Задача 13 – Стереометрия.

Задача 16 – Геометрия на плоскости.

Задача 17 – Параметры.

И задача 18 – нестандартная и ни на что не похожая.

Мы подробно рассказывали о каждой из этих задач, когда писали о структуре профильного ЕГЭ по математике.

Что делать на экзамене?

Надо посмотреть на эти 4 сложных задачи – Стереометрию, Геометрию, Параметры и Нестандартную – опытным взглядом. Если вы весь год занимались на курсах ЕГЭ или с хорошим репетитором, то одна из этих задач точно покажется вам знакомой и простой. Вы точно помните, как ее решать! Берем и делаем. Решаем, проверяем, оформляем чистовик. Затем – следующая. Следим за временем: двух с половиной часов на 4 сложных задачи вполне достаточно. Важно не «зависать»! Если у вас 10 минут нет никаких идей по решению – переходите к следующей.

Самые «дорогостоящие» из этих задач – это номера 18 и 19. Они оцениваются в 4 первичных балла каждая, и эти 4 первичных пересчитываются в 8-9 тестовых. Так что если вы решили три из четырех сложных задач на профильном ЕГЭ по математике – вы чемпион!

Удачи вам на ЕГЭ по математике!

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Как распределить время на ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.03.2023

Распределительное свойство

: 5 эффективных примеров использования в классе

Что такое распределительное свойство ? Также известный как распределительный закон умножения, это одно из наиболее часто используемых свойств в математике.

Когда вы что-то распространяете, вы делите это на части. В математике свойство дистрибутивности помогает упростить сложные задачи, поскольку оно разбивает выражения на сумму или разность двух чисел.

В соответствии с этим принципом, умножение суммы двух слагаемых на число даст нам точно такой же результат, как и умножение каждого слагаемого по отдельности на число, а затем их сложение.

Понимание распределительного свойства

Для выражений в форме a(b+c) распределительное свойство показывает нам, как их решать с помощью: внутри

Как насчет PEMDAS? Что случилось с первой оценкой того, что находится внутри скобок?

Если ваши ученики задаются вопросом, почему вы не следуете тому порядку операций, которому их учили в прошлом, они не ошибаются.

Однако, когда алгебраические выражения имеют круглые скобки, содержащие переменные — количество, которое может измениться в контексте математической задачи, обычно представленное одной буквой — выполнение этой операции невозможно.

Распределительное свойство умножения над сложением

Независимо от того, используете ли вы распределительное свойство или следуете порядку операций, вы получите один и тот же ответ. В первом примере ниже мы просто оцениваем выражение в соответствии с порядком операций, упрощая сначала то, что было в скобках.

Используя закон распределения, мы:

1. Умножаем или распределяем внешний член на внутренние члены.
2. Объедините похожие термины.
3. Решите уравнение.

Давайте используем сценарий из реальной жизни в качестве примера распределительного свойства.

Представьте, что у одной ученицы и двух ее друзей есть по семь ягод клубники и четыре клементина. Сколько всего фруктов у всех трех учеников?

В их пакетах с обедом — или, в скобках — у каждого из них по 7 клубник и 4 клементина. Чтобы узнать общее количество кусочков фруктов, им нужно умножить все это на 3.

Разбивая его, вы умножаете 7 ягод клубники и 4 клементина на 3 учащихся. Итак, у вас получится 21 клубника и 12 клементинов, всего 33 фрукта.

Распределительное свойство умножения на вычитание

Подобно предыдущей операции, выполнение распределительного свойства с вычитанием следует тем же правилам, за исключением того, что вы находите разность вместо суммы.

Примечание : Не имеет значения, положительная или отрицательная операция. Оставьте то, что в скобках.

Распределительное свойство с переменными

Помните, что мы говорили об алгебраических выражениях и переменных? Распределительное свойство позволяет нам упростить уравнения при работе с неизвестными значениями.

Используя закон распределения с задействованными переменными, мы можем изолировать x :

1. Умножить или распределить внешний член на внутренние члены.
2. Объедините похожие термины.
3. Расположите термины так, чтобы константы и переменные находились по разные стороны от знака равенства.
4. Решите уравнение и при необходимости упростите его.

Примечание : При изоляции переменных (см. третий шаг) то, что вы делаете с одной стороной, вы должны делать и с другой. Чтобы исключить 12 с левой стороны, вы должны добавить по двенадцать и к левой, и к правой стороне. То же самое касается умножения и деления: чтобы изолировать x , разделите каждую сторону на 4.

Распределительное свойство с показателями степени

Показатель степени — это сокращенная запись, показывающая, сколько раз число умножается само на себя. Когда скобки и показателей степени, использование распределительного свойства может значительно упростить выражение.

1. Расширьте уравнение.
2. Умножьте (распределите) первые числа каждого набора, внешние числа каждого набора, внутренние числа каждого набора и последние числа каждого набора.
3. Объедините похожие термины.
4. Решите уравнение и при необходимости упростите его.

Примечание : На втором этапе используйте метод FOIL (первое, внешнее, внутреннее, последнее) для распределения каждого выражения.

Распределительное свойство с дробями

Решение алгебраических выражений с дробями выглядит сложнее, чем есть на самом деле. Выполните шаги, описанные ниже, чтобы увидеть, как это делается.

Надеемся, что этот пошаговый процесс поможет вашим учащимся понять, как и почему свойство дистрибутивности может пригодиться при упрощении дробей и комплексных чисел.

1. Определите дроби. Используя свойство распределения, вы в конечном итоге превратите их в целые числа.
2. Для всех дробей найдите наименьшее общее кратное (НОК) — наименьшее число, в которое могут точно вписаться оба знаменателя. Это позволит вам добавлять дроби.
3. Умножьте каждый член уравнения на НОК.
4. Изолировать переменные, добавляющие или вычитающие одинаковые термины по обе стороны от знака равенства.
5. Объедините похожие термины.
6. Решите уравнение и при необходимости упростите его.

Примечание : На шагах два и три мы находим НОК и используем его для умножения дробей, чтобы упростить их и избавиться от них. Нужна быстрая переподготовка? См. статью в нашем блоге о том, как умножать дроби.

Разнообразные свойства

Помимо распределительного свойства, существуют и другие часто используемые свойства, такие как ассоциативное свойство и коммутативное свойство.

Давайте посмотрим на ассоциативное свойство:

Ассоциативное свойство относится к группированию элементов вместе. Это правило гласит, что то, как числа (или целые числа) сгруппированы в математической задаче, не изменит результат.

Дополнительный пример:

a + (b +c) = (a + b) + c или 2 + (3 + 4) = (2 + 3) + 4

Пример умножения:

5×4×2 = ( 5 x 4) x 2 = 20 x 2 = 40

Это свойство работает с умножением, сложением, вычитанием и делением.

Различные способы изучения дистрибутивной собственности

1. Prodigy

Prodigy — это адаптивная обучающая математическая платформа на основе игр, которую любят более миллиона учителей и 150 миллионов учащихся по всему миру! Он предлагает материалы, соответствующие учебной программе, по всем основным математическим темам в 1–8 классах, в том числе инструкции:

• Используйте распределительное свойство для расширения и решения выражений
• Заполните пропущенные числа в эквивалентных выражениях, используя распределительное свойство

Использование Prodigy Math Game может помочь учащимся изучать и практиковать математику за пределами фактической беглости и до второго и третьего уровней DoK . Ответив на такие вопросы, как приведенный выше, учащиеся получат массу удовольствия, пока будут практиковать распределительное свойство.

Хотите дополнить уроки математики увлекательной игровой платформой для обучения и мощными инструментами для учителей?

Зарегистрируйтесь сейчас, чтобы получить бесплатную учетную запись учителя

2. Словесные задачи

Свойство дистрибутивности может оказаться неприменимым к повседневной жизни, но давайте посмотрим на него в действии через некоторые словесные задачи!

У Лиама разносторонний музыкальный вкус. Просматривая музыку на своем телефоне, друзья Лиама находят песни трех разных жанров: поп, металл и кантри. Металлических песен в шесть раз больше, чем поп-песен, и кантри-песен в 11 раз больше, чем поп-песен. Если x представляет собой количество поп-песен, сколько всего песен у Лиама в телефоне? Напишите выражение. Упрощать.

Чтобы получить количество металлических песен, умножьте количество поп-песен на пять — 5x .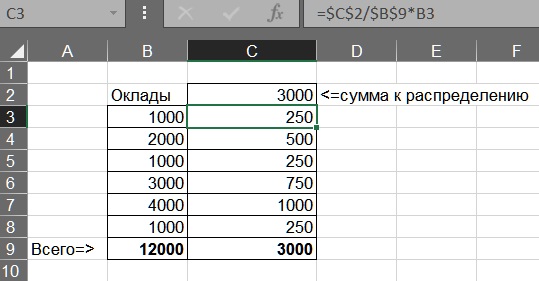 Чтобы получить количество кантри-песен, умножьте количество поп-песен на 11 — 11x . Поскольку вы знаете, что x — это количество поп-песен, вы можете написать выражение как:

Школьный тренер по футболу снабжает свою команду новой формой: майкой, парой шорт и щитками для голеней. Одна футболка стоит 15 долларов, пара шорт — 11 долларов, а комплект щитков — 8 долларов.

Сколько стоит форма на одного товарища по команде? Напишите выражение и упростите.

Сколько всего будет стоить, если в команде 11 игроков? Напишите выражение и упростите.

3. Массивы

Визуальные или практические манипуляции помогают учащимся разобраться в математике и конкретизировать абстрактные понятия. Они особенно полезны для углубления понимания вашими учащимися свойства распределения.

Используйте предметы, картинки, цифры — что угодно! — в строках и столбцах как полезный способ представления математических выражений, таких как 4×5 и 5×9. Взгляните на приведенный ниже пример на Indulgy:

Разбивая выражения на маленькие кусочки, учащиеся могут решать более крупные и сложные математические задачи. Вот где распределительная собственность помогает.

Если ребенок не может ответить на 45, используйте массивы меньшего размера и перепишите выражение как 4(3+2) или 4(3)+4(2). Это четыре строки по три плюс четыре строки по два , что соответствует массиву из 9.0003 четыре ряда по пять .

Заключительные мысли о свойстве распределения

Как одно из наиболее часто используемых свойств, важно научиться выполнять и применять свойство распределения. Без него очистка скобок была бы невозможна.

Включив ресурсы EdTech, массивы или математические задачи, учащиеся должны увидеть практическое практическое применение свойства распределения.

Сработал ли один пример более эффективно, чтобы привлечь учащихся и углубить их понимание? Есть только один способ узнать это — попробовать!

Prodigy Math Game — это игровая платформа для обучения математике, которую легко использовать как преподавателям, так и учащимся. В соответствии с учебными планами англоязычного мира ваша бесплатная учетная запись учителя дает вам доступ к инструментам, которые помогают с дифференциацией, мотивацией и оценками.

Зарегистрируйте бесплатную учетную запись

Распространяемая собственность | ChiliMath. Следующая диаграмма иллюстрирует основной шаблон или формулу, как ее применять.

Несколько примечаний:

• Это делается путем умножения внешнего члена на каждый член в скобках.

• Итак, возьмем терм a, находящийся вне скобок, и распределим его по каждому терму внутри скобок.

• Обратите внимание, что ab означает a, умноженное на b.

• Аналогично, ac означает a, умноженное на c.

Объединение похожих терминов с использованием распространяемого свойства

Пример 1: Распределить, затем упростить приведенное ниже выражение.

Можно ли сразу объединить x-термины? Не так быстро! Термин 2x находится внутри скобок, а 3x снаружи. Мы не можем их объединить, потому что они находятся в разных местах.

Что нам нужно сделать, так это сначала исключить символ скобки, прежде чем мы сможем комбинировать одинаковые термины, которые возникнут при добавлении или вычитании. Вот где полезность этого свойства вступает в игру.

На этом этапе скобки больше нет, и все x-термины можно комбинировать. Я бы переставил их, разместив похожие термины рядом, прежде чем выполнять требуемую операцию.

Пример 2: Распределите, затем упростите приведенное ниже выражение.

Так как здесь две круглые скобки, мы должны применить это свойство дважды. Это должно избавиться от группирующих символов и позволить нам комбинировать похожие термины.

После удаления двух скобок теперь можно комбинировать одинаковые термины. Перед выполнением необходимой операции сложения или вычитания обязательно переставьте термины таким образом, чтобы похожие термины располагались рядом.

Пример 3: Распределить, затем упростить приведенное ниже выражение.

Надеюсь, теперь вы видите схему. Имея три круглых скобки, мы также должны применить их три раза.

Поскольку все термины теперь не в скобках, продолжайте комбинировать похожие термины.

Пример 4: Распределить, затем упростить приведенное ниже выражение.

Решение:

Пример 5: Распределите, затем упростите приведенное ниже выражение.

Решение:

Пример 6: Распределите, затем упростите приведенное ниже выражение.

Решение:

Сначала примените распределительное свойство к внутренним скобкам, а затем объедините одинаковые термины. Наконец, избавьтесь от символа квадратной скобки, раздав еще раз.

Вы также можете использовать Распределительное свойство при решении уравнений .

Решение линейных уравнений с использованием распределительного свойства

Пример 7: Решите приведенное ниже линейное уравнение, используя Распределительное свойство.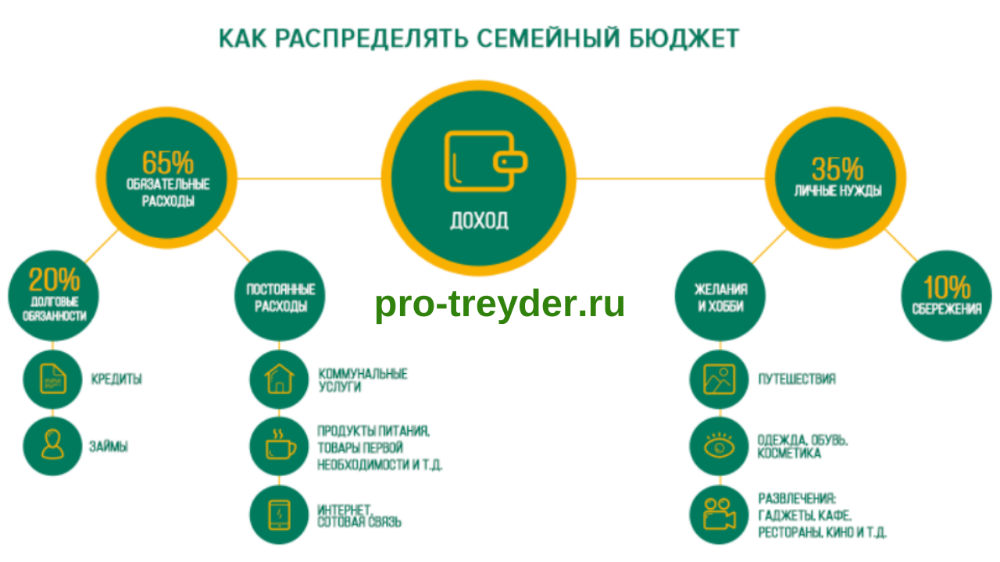

Как видите, внешнее число 3, расположенное непосредственно слева от круглой скобки, предполагает, что мы можем применить это свойство для устранения символа группировки.

• Возьмите это число 3 и умножьте на каждый член в скобках.

• После этого символ скобки должен исчезнуть. Затем мы можем приступить к обычным шагам решения уравнения. В этом примере мы изолируем переменную «x» слева от уравнения. После распределения вычтите обе части на 3, а затем разделите -\,6 на обе стороны уравнения, чтобы получить окончательный ответ.

Пример 8: Решите приведенное ниже линейное уравнение, используя Распределительное свойство.

Наличие двух скобок в левой части уравнения означает, что мы должны распределять дважды.

Избавившись от группирующих символов, теперь мы можем комбинировать одинаковые термины и изолировать переменную в левой части уравнения.

Пример 9: Используйте Распределительное свойство для решения уравнения.

This entry was posted in Популярное