Содержание
07.3. Примеры статистических моделей и гипотез, ранги и ранжирование
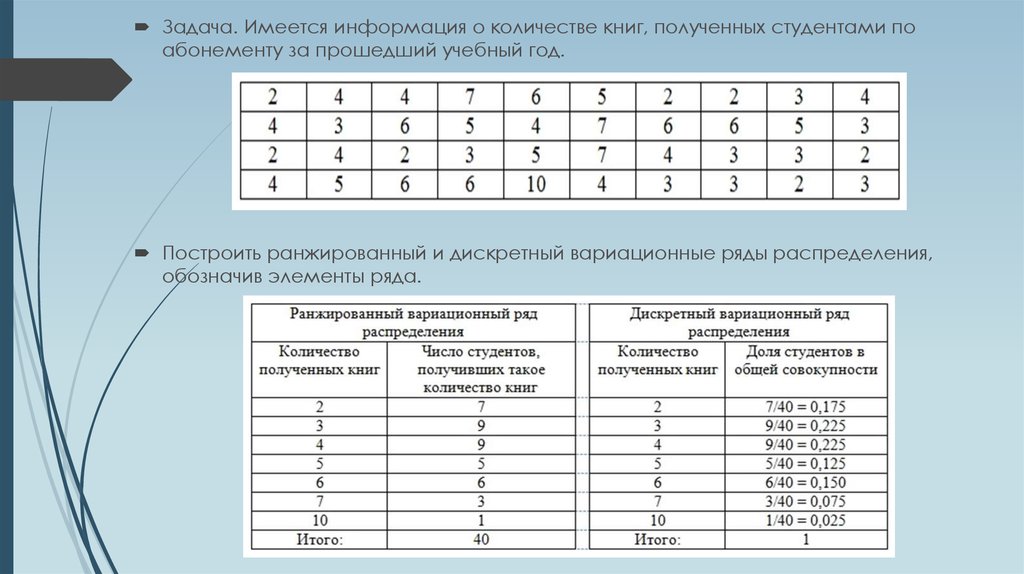
Ранги. Во многих случаях имеющиеся в нашем распоряжении числовые данные (например, значения элементов выборки) носят в той или иной мере условный характер. Например, эти данные могут быть тестовыми баллами, экспертными оценками, данными о вкусовых или политических предпочтениях опрошенных людей и т. д. Анализ таких данных требует особой осторожности, поскольку многие предпосылки классических статистических методов (например, предположения о каком-либо конкретном, скажем нормальном, законе распределения) для них не выполняются. Твердую основу для выводов здесь дают только соотношения между наблюдениями типа «больше-меньше», так как они не меняются при изменении шкалы измерений. Например, при анализе анкет с данными о симпатиях избирателей к политическим деятелям мы можем сказать, что политик, получивший больший балл в анкете, более симпатичен отвечавшему на вопросы человеку (респонденту), чем политик, получивший меньший балл. Но на сколько (или во сколько раз) он более симпатичен, сказать нельзя, так как для предпочтений нет объективной единицы измерения.
Но на сколько (или во сколько раз) он более симпатичен, сказать нельзя, так как для предпочтений нет объективной единицы измерения.
В подобных случаях (которые мы будем более подробно рассматривать в последующих главах), имеет смысл вообще отказаться от анализа конкретных значений данных, а исследовать только информацию об из взаимной упорядоченности. Для этого от исходных числовых данных осуществляют переход к их Рангам.
Определение. Рангом наблюдения называют тот номер, который получит это наблюдение в упорядоченной совокупности всех данных — после их упорядочения по определенному правилу (например, от меньших значений к большим или наоборот).
Чаще всего упорядочение чисел (набор которых составляют упомянутые выше данные) производят по величине — от меньших к большим. Именно такое упорядочение и связанное с ним ранжирование (присвоение рангов) мы будем иметь в виду в дальнейшем.
Пример. Пусть выборка состоит из чисел 6, 17, 14,5, 12. Тогда рангом числа 6 оказывается 2, рангом 17 будет 5 и т. д.
Тогда рангом числа 6 оказывается 2, рангом 17 будет 5 и т. д.
Определение. Процедура перехода от совокупности наблюдений к последовательности их рангов называется ранжированием. Результат ранжирования называется ранжировкой.
Статистические методы, в которых мы делаем выводы о данных на основании их рангов, называются ранговыми. Они получили широкое распространение, так как надежно работают при очень слабых предположениях об исходных данных (не требуя, например, чтобы эти данные имели какой-либо конкретный закон распределения). В последующих главах этой книги мы рассмотрим применение ранговых методов в наиболее распространенных практических задачах.
Средние ранги. Трудности в назначении рангов возникают, если среди элементов выборки встречаются совпадающие. (Так часто бывает, когда данные регистрируются с округлением.) В этом случае обыкновенно используют Средние ранги.
Средние ранги вводятся так. Предположим, что наблюдение , имеет ту же величину, что и некоторые другие из общего числа П Наблюдений. (Эту совокупность одинаковых наблюдений из набора называют Связкой, количество таких одинаковых наблюдений в данной связке называют ее размером.) Средний ранг , в ранжировке наблюдений есть среднее арифметическое тех рангов, которые были бы назначены и всем остальным элементам связки, если бы одинаковые наблюдения оказались различны.
(Эту совокупность одинаковых наблюдений из набора называют Связкой, количество таких одинаковых наблюдений в данной связке называют ее размером.) Средний ранг , в ранжировке наблюдений есть среднее арифметическое тех рангов, которые были бы назначены и всем остальным элементам связки, если бы одинаковые наблюдения оказались различны.
В качестве примера рассмотрим выборку 6, 17, 12, 6, 12. Ее ранжировка равна .
Покажем на примерах, как может проходить математическая формализация практических задач и как сформулированные на естественном языке вопросы превращаются в статистические гипотезы.
Тройной тест. Рассмотрим распространенный в психологии тройной тест (его другое название — тест дегустатора). Он состоит из серии одинаковых опытов, в каждом из которых испытуемому предъявляют одновременно три стимула. Два из них идентичны, а третий несколько отличается. Испытуемый, ориентируясь на свои ощущения, должен указать этот отличающийся стимул. Например, испытуемому могут быть предложены три стакана с жидкостью: два с чистой водой, а третий — со слабым раствором сахара, либо наоборот — два стакана подслащенных, а третий — с чистой водой. Задание для испытуемого — указать стакан, отличающийся от двух других.
Задание для испытуемого — указать стакан, отличающийся от двух других.
Опыты стараются организовать так, чтобы они проходили в одинаковых условиях и чтобы в каждом из них испытуемый мог полагаться только на свои ощущения. В результате подобного однократного эксперимента можно получить как правильный, так и неправильный ответ.
При слабой концентрации раствора, когда его трудно отличить от воды, из одного ответа нельзя сделать определенного заключения о способности испытуемого чувствовать данную концентрацию. Испытуемый может случайно ошибиться, даже если в целом он способен отличать данную концентрацию сахара от чистой воды. С другой стороны, правильный ответ не исключает того, что испытуемый его просто угадал, не отличая раствора от воды.
Эти свойства эксперимента мы можем перечислить в виде следующих допущений:
• в каждом испытании ответ испытуемого случаен;
• существует вероятность правильного ответа, которая неизменна во все время испытаний;
• результаты отдельных испытаний статистически независимы.
Коротко это выражается так: статистической моделью эксперимента служит схема Бернулли.
Сформулировав математическую модель явления, перейдем к выдвижению статистических гипотез. Интересующая нас способность испытуемого характеризуется вероятностью правильного ответа, которую мы обозначим Р. В этом опыте она нам неизвестна. Естественно, эта вероятность зависит от степени концентрации сахара. Если концентрация очень мала и не воспринимается, то у испытуемого нет оснований для выбора. Он «наудачу» будет указывать один из трех стаканов. В этих условиях вероятность правильного ответа .
Предположим, что экспериментатора интересует, начиная с каких концентраций испытуемый отличает раствор от воды. Тогда для данной концентрации экспериментатор может выдвинуть предположение, что испытуемый ее ощутить не в состоянии. В изложенной модели это предположение превращается в статистическую гипотезу о том, что . Примем следующую форму записи статистической гипотезы: . Если же экспериментатор предполагает, что испытуемый может ощутить наличие сахара, то соответствующая статистическая гипотеза состоит в том, что , т. е. . Возможна и гипотеза о том, что , она соответствует тому, что испытуемый способен отличить раствор от воды, но принимает одно за другое.
е. . Возможна и гипотеза о том, что , она соответствует тому, что испытуемый способен отличить раствор от воды, но принимает одно за другое.
Экспериментатор может выдвигать и другие гипотезы о способности испытуемого к различению концентраций. Например, возможна такая гипотеза: испытуемый способен ощутить присутствие сахара, ошибаясь один раз из десяти. В этом случае вероятность правильного ответа равна 0.9 и гипотеза примет вид: Н : р = 0.9.
Заметим, что с чисто математической точки зрения гипотеза вида проще, чем или . Действительно, при мы имеем дело с одним (полностью заданным) биномиальным распределением, а в других случаях перед нами семейство распределений. Ясно, что с одним распределением иметь дело проще.
Сейчас мы не будем рассматривать процесс проверки этих гипотез (он описан в п. 4), а вместо этого приведем еще один пример перевода естественнонаучной задачи на статистический язык, т. е. построения статистической модели явления и выдвижения гипотезы для проверки.
Парные наблюдения. На практике часто бывает необходимо сравнить два способа действий по их результатам. Речь может идти о сравнении двух методик обучения, эффективности двух лекарств, производительности труда при двух технологиях и т. д. В качестве конкретного примера рассмотрим эксперимент, в котором выясняется, на какой из сигналов человек реагирует быстрее: на свет или на звук.
Эксперимент был организован следующим образом. Каждому из семнадцати испытуемых в случайном порядке поочередно подавались два сигнала: световой и звуковой. Интенсивность сигналов была неизменна в течение всего эксперимента. Увидев или услышав сигнал, испытуемый должен был нажать на кнопку. Время между сигналом и реакцией испытуемого регистрировал прибор. Результаты эксперимента приведены в табл. 1.
Таблица 1
Время реакции на свет и на звук, в миллисекундах
|
I
|
Xi
|
Yi
|
|
1
|
223
|
181
|
|
2
|
104
|
194
|
|
3
|
209
|
173
|
|
4
|
183
|
153
|
|
5
|
180
|
168
|
|
6
|
168
|
176
|
|
7
|
215
|
163
|
|
8
|
172
|
152
|
|
9
|
200
|
155
|
|
10
|
191
|
156
|
|
11
|
197
|
178
|
|
12
|
183
|
160
|
|
13
|
174
|
164
|
|
14
|
176
|
169
|
|
15
|
155
|
155
|
|
16
|
115
|
122
|
|
17
|
163
|
144
|
I — номер испытуемого, I = 1,. .., 17; Xi — время его реакции на звук, YI — время его реакции на свет.
.., 17; Xi — время его реакции на звук, YI — время его реакции на свет.
Вместо поставленного выше вопроса о том, на какой из сигналов человек отвечает быстрее, выдвинем другой: можно ли считать, что время реакции человека на свет и на звук одинаковы? Логически эти вопросы тесно связаны: если мы отвечаем отрицательно на второй из них, мы тем самым признаем, что различия есть. После этого уже не трудно понять, когда время реакции меньше. Если же на второй вопрос мы отвечаем положительно, то первый после этого просто снимается. С математической же точки зрения второй вопрос проще, как мы увидим из дальнейшего обсуждения.
Итак, время реакции на звук, X, и время реакции на свет, Y, различно у разных людей, несмотря на то, что во время опыта они находились в одинаковых условиях. Ясно, что наблюдаемый разброс во времени реакции не связан с изучаемым явлением (различием двух действий). По-видимому, этот разброс можно объяснить различиями между испытуемыми и/или нестабильностью времени отклика на сигнал у каждого испытуемого. Как бы то ни было, эти колебания не имеют отношения к той закономерности, что нас интересует. Поэтому мы объявляем их случайными. Так сделан первый шаг к статистической модели: переменные Xi и Yi признаны реализациями случайных величин, скажем Xi и Yi. Поскольку каждый испытуемый решал свои задачи самостоятельно, не взаимодействуя с другими испытуемыми и не испытывая с их стороны влияния, мы будем считать случайные величины X1, Y1,…, Х17, Y17 Независимыми (в теоретико-вероятностном смысле).
Как бы то ни было, эти колебания не имеют отношения к той закономерности, что нас интересует. Поэтому мы объявляем их случайными. Так сделан первый шаг к статистической модели: переменные Xi и Yi признаны реализациями случайных величин, скажем Xi и Yi. Поскольку каждый испытуемый решал свои задачи самостоятельно, не взаимодействуя с другими испытуемыми и не испытывая с их стороны влияния, мы будем считать случайные величины X1, Y1,…, Х17, Y17 Независимыми (в теоретико-вероятностном смысле).
Выбор статистической модели. Дальнейшее уточнение статистической модели в подобных задачах может идти различными путями, в зависимости от природы эксперимента и наших знаний о ней. Один путь связан с предположением о том, что случайные величины XI и Yi имеют некоторые конкретные законы распределения. Например, мы можем предположить, что Xi и Yi — независимы и имеют нормальные распределения с одной и той же дисперсией (обозначим ее ). Тогда, если ввести для средних значений обозначения: где I = 1,…, 17, то можно сформулировать наши допущения так: случайные величины Xi, Yi подчиняются нормальным распределениям Соответственно, где параметры нам неизвестны. При этих обозначениях выдвинутый вопрос о равном времени реакции на свет и на звук может быть сформулирован как статистическая гипотеза:
Тогда, если ввести для средних значений обозначения: где I = 1,…, 17, то можно сформулировать наши допущения так: случайные величины Xi, Yi подчиняются нормальным распределениям Соответственно, где параметры нам неизвестны. При этих обозначениях выдвинутый вопрос о равном времени реакции на свет и на звук может быть сформулирован как статистическая гипотеза:
Если экспериментатор уверен, что группа испытуемых достаточно однородна, он может дополнительно предположить, что и . Если обозначить общие значения параметров через A и B соответственно, то статистическую модель в этом случае можно сформулировать так: случайные величины независимы и распределены по закону ; случайные величины тоже независимы, не зависят от и распределены по закону . Параметры A, B и неизвестны. Тогда гипотезу о равном времени реакции можно записать следующим образом:
Ясно, что задача с меньшим числом неопределенных параметров, как во второй постановке, в принципе должна давать более точные ответы. При проверке гипотез это означает, что мы сможем принять или отвергнуть проверяемую гипотезу с большей степенью уверенности. Но следует помнить, что уменьшение количества параметров в модели является следствием принятия дополнительных предположений об имеющихся данных. Так, в приведенном выше примере мы предположили, что и , что и дало нам возможность уменьшить количество параметров в модели с 35 до 3. Но если сделанные дополнительные предположения являются неправомерными, то использование полученной математической модели может привести к неверному заключению. Например, при обработке наших данных по однородной схеме можно получить неверный ответ, если фактически эти данные однородными не являются.
При проверке гипотез это означает, что мы сможем принять или отвергнуть проверяемую гипотезу с большей степенью уверенности. Но следует помнить, что уменьшение количества параметров в модели является следствием принятия дополнительных предположений об имеющихся данных. Так, в приведенном выше примере мы предположили, что и , что и дало нам возможность уменьшить количество параметров в модели с 35 до 3. Но если сделанные дополнительные предположения являются неправомерными, то использование полученной математической модели может привести к неверному заключению. Например, при обработке наших данных по однородной схеме можно получить неверный ответ, если фактически эти данные однородными не являются.
Итак, при построении статистической модели постоянно приходится вводить упрощающие математические предположения и одновременно оценивать, насколько они приемлемы с содержательной точки зрения. И часто надо быть готовым к тому, чтобы отказаться от недопустимых предположений или заменить их чем-то другим.
Другой путь построения статистической модели — так называемый Непараметрический. Здесь мы не делаем предположений о том, что наблюдаемые случайные переменные имеют какой-либо параметрический закон распределения. В этом случае мы делаем меньше математических допущений, а значит, здесь меньше опасности принять неоправданное предположение. Зато при этом мы используем не всю информацию об имеющихся данных, а только ту ее часть, которая не зависит от конкретного вида распределения исходных данных. Например, при проверке гипотезы о равном времени реакции на свет и звук мы должны будем использовать не сами значения времен реакций Xi и Yi, а их Ранги В объединенной выборке Xi и Yi. По сравнению с параметрическим методом (если предположения о параметрическом характере случайных событий справедливы), мы получим при этом несколько менее точные выводы, но зато непараметрический метод имеет гораздо более широкую область применимости.
Итак, при построении статистической модели приходится делать ряд предположений. Большую часть этих предположений мы не проверяем (и часто даже и не можем проверить). Некоторые предположения мы Выбираем для проверки их совместимости со статистическим материалом и называем такие предположения статистическими гипотезами. НиЖе Мы расскажем, как осуществляется проверка статистических гипотез.
Большую часть этих предположений мы не проверяем (и часто даже и не можем проверить). Некоторые предположения мы Выбираем для проверки их совместимости со статистическим материалом и называем такие предположения статистическими гипотезами. НиЖе Мы расскажем, как осуществляется проверка статистических гипотез.
| < Предыдущая | Следующая > |
|---|
Правила ранжирования
«-//W3C//DTD HTML 3.2 Final//RU\»>
Правила ранжирования
-
Меньшему значению начисляется меньший ранг.
Наименьшему значению начисляется ранг 1.
Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых
значений. Например, если n=7, то наибольшее значение получит ранг 7, за
возможным исключением для тех случаев, которые предусмотрены правилом 2.
-
В случае, если несколько значений равны, им начисляется ранг, представляющий
собой среднее значение из тех рангов, которые они получили бы, если бы не были
равны.
Например, 3 наименьших значения равны 10 секундам.
Если бы мы измеряли время более точно, то эти значения могли бы различаться и
составили бы, скажем, 10.2 сек; 10.5 сек; 10.7 сек. В этом случае они получили
бы ранги, соответственно, 1, 2 и 3. Но поскольку полученные нами значения равны,
каждое из них получает средний ранг:
Допустим, следующие 2 значения равны 12 сек. Они должны были бы получить ранги 4
Они должны были бы получить ранги 4
и 5, но, поскольку они равны, то получают средний ранг:
и т.д.
-
Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле:
где N — общее количество ранжируемых наблюдений (значений).
Несовпадение реальной и расчетной сумм рангов будет свидетельствовать об ошибке,
допущенной при начислении рангов или их суммировании. Прежде чем продолжить
работу, необходимо найти ошибку и устранить ее.
Источник: Сидоренко Е. В. Методы математической обработки в психологии —
В. Методы математической обработки в психологии —
CПб.: ООО "Речь", 2001, с.52.
© Куксов А. Ю., 2005
10. Ранговые балльные тесты
Распределение населения характеризуется или определяется такими параметрами, как среднее значение и стандартное отклонение. Для асимметричных распределений нам потребуется знать другие параметры, такие как степень асимметрии, прежде чем распределение можно будет однозначно идентифицировать, но среднее значение и стандартное отклонение однозначно идентифицируют нормальное распределение. Описанный выше критерий t зависит от своей валидности при допущении, что данные происходят из нормально распределенной совокупности, и при сравнении двух групп разница между двумя выборками возникает просто потому, что они различаются только своим средним значением.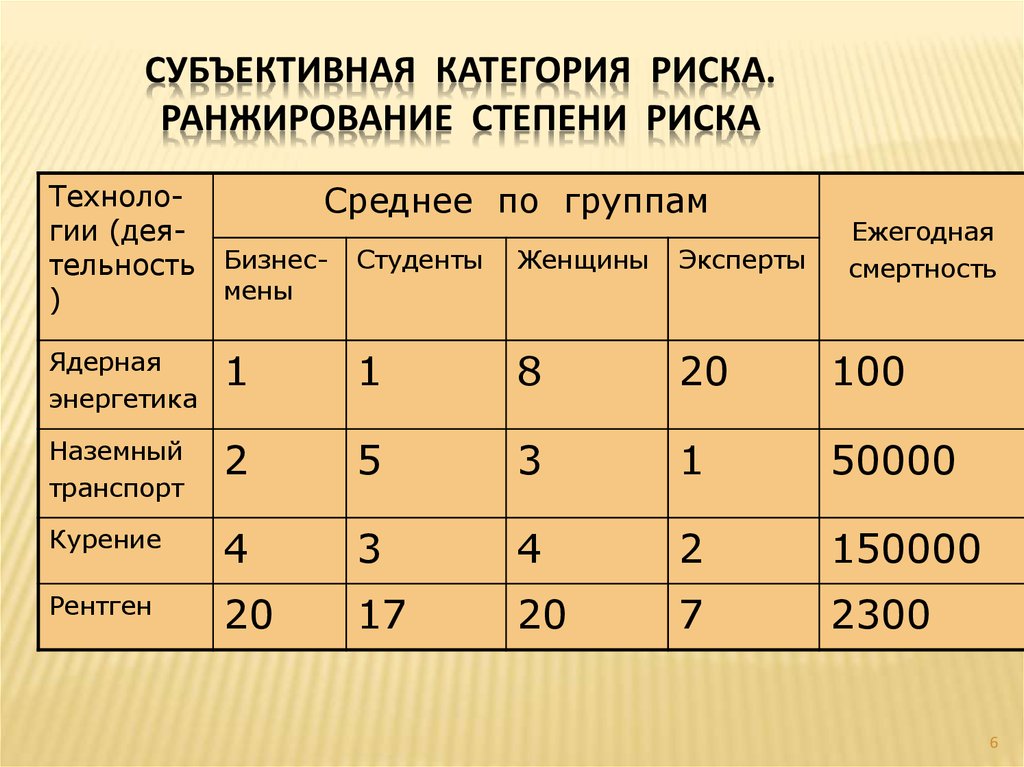 Однако, если бы мы были обеспокоены тем, что данные не получены из нормально распределенной популяции, то есть доступные тесты, которые не используют это предположение. Поскольку данные больше не имеют нормального распределения, распределение нельзя охарактеризовать несколькими параметрами, поэтому тесты часто называют «непараметрическими». Это несколько неправильное название, потому что, как мы увидим, чтобы иметь возможность сказать что-то полезное о населении, мы должны сравнивать параметры. Как упоминалось в главе 5, если размеры выборки в обеих группах велики, отсутствие нормальности вызывает меньше беспокойства, и можно применять тесты для больших выборок, описанные в этой главе.
Однако, если бы мы были обеспокоены тем, что данные не получены из нормально распределенной популяции, то есть доступные тесты, которые не используют это предположение. Поскольку данные больше не имеют нормального распределения, распределение нельзя охарактеризовать несколькими параметрами, поэтому тесты часто называют «непараметрическими». Это несколько неправильное название, потому что, как мы увидим, чтобы иметь возможность сказать что-то полезное о населении, мы должны сравнивать параметры. Как упоминалось в главе 5, если размеры выборки в обеих группах велики, отсутствие нормальности вызывает меньше беспокойства, и можно применять тесты для больших выборок, описанные в этой главе.
Уилкоксон подписал тест суммы рангов
Уилкоксон и Манн и Уитни описали тесты суммы рангов, которые оказались одинаковыми. Теперь Конвенция приписала тест Уилкоксона парным данным, а U-критерий Манна-Уитни — непарным данным.
Boogert et al (1) (данные также приведены в Shott (2) использовали УЗИ для записи движений плода до и после биопсии ворсин хориона. Процент времени, в течение которого плод двигался, приведен в таблице 10.1 для десяти беременных женщин.
Процент времени, в течение которого плод двигался, приведен в таблице 10.1 для десяти беременных женщин.
Если мы обеспокоены тем, что различия в процентах времени, проведенного в движении, вряд ли будут нормально распределены, мы могли бы использовать критерий знакового ранга Уилкоксона, используя следующие предположения:
- Парные различия независимы.
- Различия возникают из-за симметричного распределения.
Нам не нужно проводить тест, чтобы убедиться, что различия исходят из
симметричного распределения: будет достаточно теста «на глаз». График разностей в столбце (4) таблицы 10.1 приведен на рисунке 10.1. и показывает, что распределение различий правдоподобно симметрично. Затем различия ранжируются в столбце 5 (отрицательные значения игнорируются, а нулевые значения опускаются). Когда два или более различия идентичны, каждому из них присваивается балл посередине между рангами, которые они заполнили бы, если бы были различными, независимо от знака плюс или минус.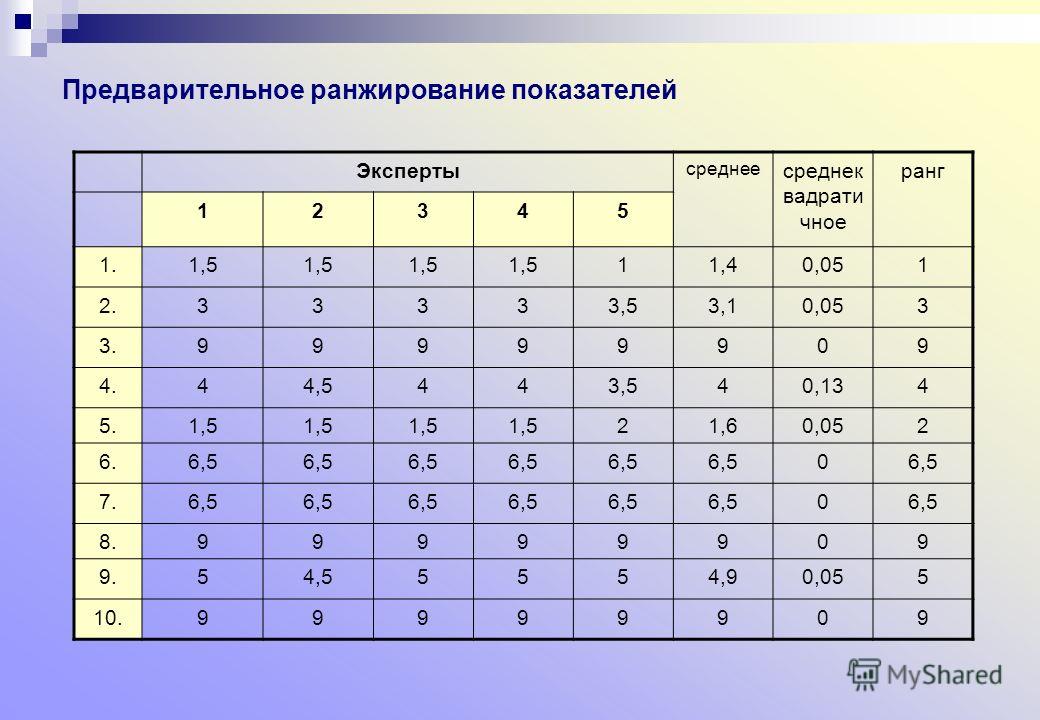 Например, различия -1 (пациент 6) и +1 (пациент 9) занимают ранги 1 и 2. Поскольку (1 + 2)/2 = 1,5, им присваивается ранг 1,5. В столбце (6) ранги повторяются для столбца (5), но каждому присваивается знак отличия от столбца (4). Полезной проверкой является то, что сумма рангов должна составлять n(n + 1)/2. В этом случае 10(10 + 1)/2 = 55.
Например, различия -1 (пациент 6) и +1 (пациент 9) занимают ранги 1 и 2. Поскольку (1 + 2)/2 = 1,5, им присваивается ранг 1,5. В столбце (6) ранги повторяются для столбца (5), но каждому присваивается знак отличия от столбца (4). Полезной проверкой является то, что сумма рангов должна составлять n(n + 1)/2. В этом случае 10(10 + 1)/2 = 55.
Числа, представляющие положительные и отрицательные ранги в столбце (6), складываются отдельно, и используется только меньшая из двух сумм. Сумма, независимо от знака, относится к Таблице Приложения D.pdf
против количества пар, использованных в расследовании. Сумма рангов больше, чем в таблице, незначима на показанном уровне вероятности. В этом случае меньший из рангов равен 23,5. Это больше, чем число (8), указанное для десяти пар в таблице D, поэтому результат не имеет значения. Доверительный интервал для интервала описан Кэмпбеллом и Гарднером (2) и Гарднером и Альтманом (4). и легко получается из программ CIA(5) или MINITAB. (6) Средняя разница равна нулю.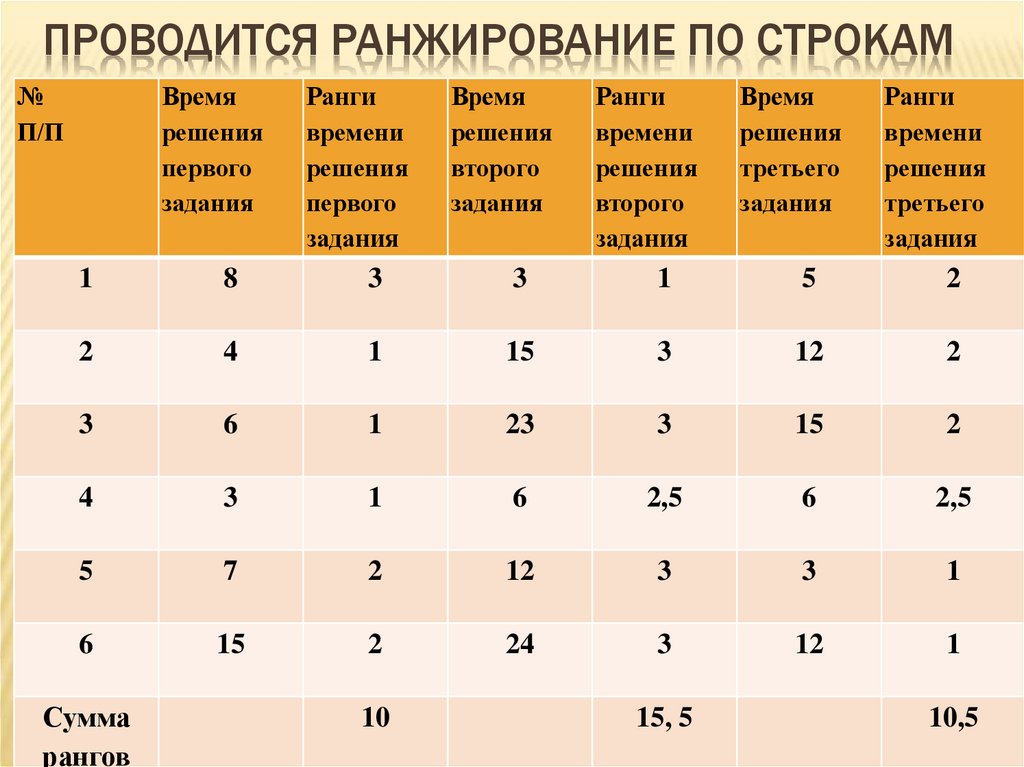 ЦРУ дает 95% доверительный интервал как от – 2,50 до 4,00. Это довольно узкое исследование, поэтому из этого небольшого исследования мы можем сделать вывод, что у нас мало доказательств того, что биопсия ворсин хориона изменяет движения плода.
ЦРУ дает 95% доверительный интервал как от – 2,50 до 4,00. Это довольно узкое исследование, поэтому из этого небольшого исследования мы можем сделать вывод, что у нас мало доказательств того, что биопсия ворсин хориона изменяет движения плода.
Обратите внимание, возможно, вопреки интуиции, что критерий Уилкоксона, хотя и является ранговым критерием, может дать другое значение, если данные будут преобразованы, скажем, путем логарифмирования. Таким образом, возможно, стоит построить график распределения различий для ряда преобразований, чтобы увидеть, делают ли они распределение более симметричным.
Непарные образцы
Старший регистратор ревматологической клиники районной больницы разработал клиническое исследование нового препарата для лечения ревматоидного артрита.
Двадцать пациентов были рандомизированы в две группы по десять человек для получения либо стандартной терапии A, либо нового лечения B. Фракции глобулинов плазмы после лечения перечислены в таблице 10. 2
2
Мы хотим проверить, изменило ли новое лечение плазму глобулин, и нас беспокоит предположение о Нормальности.
Первым шагом является построение графика данных (см. рис. 10.2).
Клиницист был обеспокоен отсутствием нормальности основного распределения данных и поэтому решил использовать непараметрический тест. Подходящим тестом является U-критерий Манна-Уитни, который рассчитывается следующим образом.
Наблюдения в двух выборках объединяются в одну серию и ранжируются по порядку, но при ранжировании цифры одной выборки должны отличаться от цифр другой. Данные выглядят так, как указано в таблице 10.3. Для экономии места они были размещены в двух столбцах, но ранжирование выполнено в одинарном порядке. Цифры для образца В выделены жирным шрифтом. Снова сумма рангов равна n(n + 1)/2.
Сумма рангов: образец А, 81,5; образец B, 128,5
Ранги для двух образцов теперь добавляются отдельно, и используется меньшая сумма. Он упоминается в Таблице Приложения E.pdf, равной количеству наблюдений в одной выборке и равному количеству наблюдений в другой выборке. В этом случае они оба равны 10. При = 10 и = 10 в верхней части таблицы отображается цифра 78. Меньшая сумма рангов равна 81,5. Поскольку это немного больше, чем 78, оно не достигает уровня вероятности 5%. Следовательно, на этом уровне результат не является значимым. В нижней части , где приведены цифры для 1% уровня вероятности, цифры для = 10 и
Он упоминается в Таблице Приложения E.pdf, равной количеству наблюдений в одной выборке и равному количеству наблюдений в другой выборке. В этом случае они оба равны 10. При = 10 и = 10 в верхней части таблицы отображается цифра 78. Меньшая сумма рангов равна 81,5. Поскольку это немного больше, чем 78, оно не достигает уровня вероятности 5%. Следовательно, на этом уровне результат не является значимым. В нижней части , где приведены цифры для 1% уровня вероятности, цифры для = 10 и
= 10 равно 71. Как и ожидалось, результат дальше от этого, чем 5%-ное число 78. в том, что один кажется сдвинутым влево или вправо от другого. Это означает, например, что мы не ожидаем, что одна выборка будет сильно смещена вправо, а другая — влево. Если предположение разумно, то можно рассчитать доверительный интервал для средней разницы. (3, 4) Обратите внимание, что компьютерная программа вычисляет не разницу в медианах, а скорее медиану всех возможных различий между двумя выборками. Это обычно близко к медианной разнице и имеет теоретические преимущества. Из CIA мы находим, что разница в медианах составляет -5,5, а приблизительно 95% доверительный интервал составляет – от 10 до 1,0. Как и следовало ожидать из теста значимости, этот интервал включает ноль. Хотя этот результат не является значимым, было бы неразумно делать вывод об отсутствии доказательств того, что методы лечения А и В различались, поскольку доверительный интервал довольно широк. Это говорит о том, что следует планировать более масштабное исследование.
Из CIA мы находим, что разница в медианах составляет -5,5, а приблизительно 95% доверительный интервал составляет – от 10 до 1,0. Как и следовало ожидать из теста значимости, этот интервал включает ноль. Хотя этот результат не является значимым, было бы неразумно делать вывод об отсутствии доказательств того, что методы лечения А и В различались, поскольку доверительный интервал довольно широк. Это говорит о том, что следует планировать более масштабное исследование.
Если две выборки имеют разный размер, после ранжирования, как в таблице 10.3, необходим дополнительный расчет.
Пусть = количество пациентов или объектов в меньшей выборке и общее количество рангов для этой выборки. Пусть количество пациентов или объектов в большей выборке. Затем вычислить
из следующей формулы:
Наконец, введите в таблицу E меньшее из или
Как и прежде, значимыми являются только итоги, меньшие критических точек. См. Упражнение 10.2 для примера этого метода.
См. Упражнение 10.2 для примера этого метода.
Если есть только несколько связей, то есть если два или более значений в данных равны (скажем, менее 10% данных), то для размеров выборки вне диапазона мы можем вычислить
При нулевой гипотезе, что две выборки взяты из одной и той же совокупности, z примерно нормально распределено, среднее значение равно нулю, а стандартное отклонение равно единице, и его можно использовать в таблице приложения A.pdf для расчета значения P.
Из данных таблицы 10.2 мы получаем
и из таблицы приложения A.pdf мы находим, что P составляет около 0,075, что подтверждает предыдущий результат.
Преимущества этих тестов, основанных на ранжировании, заключаются в том, что их можно безопасно использовать на данных, которые не имеют нормального распределения, что их можно быстро выполнить и что калькулятор не нужен. Данные с ненормальным распределением иногда можно преобразовать с помощью логарифмирования или какого-либо другого метода, чтобы сделать их нормально распределенными, и выполнить контрольную проверку. Следовательно, наилучшая процедура для принятия может потребовать тщательного обдумывания. Степень и характер различий между двумя выборками часто более четко выявляются с помощью стандартных отклонений и t-тестов, чем с помощью непараметрических тестов.
Следовательно, наилучшая процедура для принятия может потребовать тщательного обдумывания. Степень и характер различий между двумя выборками часто более четко выявляются с помощью стандартных отклонений и t-тестов, чем с помощью непараметрических тестов.
Общие вопросы
Непараметрические тесты действительны как для ненормально распределенных данных, так и для нормально распределенных данных, так почему бы не использовать их постоянно?
Было бы разумно использовать непараметрические тесты во всех случаях, что избавило бы от необходимости проверять нормальность. Однако параметрические тесты предпочтительнее по следующим причинам:
- 1. Как я пытался подчеркнуть в этой книге, нас редко интересуют только тесты значимости; мы хотели бы сказать что-то о генеральной совокупности, из которой были получены выборки, и это лучше всего сделать с помощью оценок параметров и доверительных интервалов.
- 2. Гибкое моделирование с непараметрическими тестами, например, с учетом смешанных факторов с использованием множественной регрессии, выполнять сложно (см.
 главу 11).
главу 11).
Сравнивают ли непараметрические тесты медианы?
Широко распространено мнение, что U-критерий Манна-Уитни на самом деле является критерием различий в медианах. Однако две группы могут иметь одинаковую медиану и, тем не менее, иметь значимый U-критерий Манна-Уитни. Рассмотрим следующие данные для двух групп по 100 наблюдений в каждой. Группа 1: 98 (0), 1, 2; Группа 2: 51 (0), 1, 48 (2). Медиана в обоих случаях равна 0, но по критерию Манна-Уитни P < 0,000 1,
распределение данных в одной группе просто смещено на фиксированную величину от другой) можно ли сказать, что тест является тестом разницы медиан. Однако, если группы имеют одинаковое распределение, то изменение местоположения сместит медианы и средние значения на одинаковую величину, и поэтому разница в медианах будет такой же, как разница в средних. Таким образом, U-критерий Манна-Уитни также является тестом на различие средних.
Как U-критерий Манна-Уитни связан с t-тестом?
Если бы кто-то ввел ранги данных, а не сами данные в программу t-теста с двумя выборками, полученное значение P было бы очень близко к значению, полученному с помощью U-критерия Манна-Уитни.
Ссылки
- Boogert A, Manhigh A, Visser GHA. Непосредственное влияние хронического забора ворсинок на движения плода. Am J Obstet Gynecol 1987; 157:137-9.
- Shott S. Статистика для медицинских работников. Филадельфия: У. Б. Сондерс, 19 лет.90.
- Кэмпбелл М.Дж., Гарднер М.Дж. Расчет доверительных интервалов для некоторых непараметрических анализов. БМЖ 1988; 296:1369-71.
- Гарднер М.Дж., Альтман Д.Г. Статистика с уверенностью. Доверительные интервалы и статистические рекомендации. Лондон: BMJ Publishing Group, 1989.
- Gardner MJ, Gardner SB, Winter PD. CIA (анализ доверительного интервала). Лондон: BMJ Publishing Group, 1989.
- Райан Б.Ф., Джойнер Б.Л., Райан Т.А. Справочник по Minitab, 2-е изд. Бостон: Даксбери Пресс, 1985. 9.0016
Упражнения
10.1 Введено новое средство в виде таблеток для профилактики мигрени, которые следует принимать перед надвигающимся приступом. Двенадцать пациентов соглашаются попробовать это средство в дополнение к обычным общим мерам, которые они принимают, при условии, что их врач также даст совет относительно приема анальгетиков.
Перекрестное исследование с идентичными таблетками плацебо проводится в течение 8 месяцев. Количество приступов, испытанных каждым пациентом, во-первых, на новом лечении и, во-вторых, на плацебо, было следующим: пациент (1) 4 и 2; пациент (2) 12 и 6; пациент (3) 6 и 6; пациент (4) 3 и 5; пациент (5) 15 и 9; пациент (6) 10 и 11; пациент (7) 2 и 4; пациент (8) 5 и 6; пациент (9) 11 и 3; пациент (10) 4 и 7; пациент (11) 6 и 0; пациент (12) 2 и 5. В тесте суммы рангов Уилкоксона какова меньшая сумма рангов? Значимо ли это на уровне 5%?
10.2 Другой врач провел аналогичное пилотное исследование с этим препаратом на 12 пациентах, дав такое же плацебо 10 другим пациентам. Количество приступов мигрени, перенесенных пациентами в течение 6 месяцев, было следующим.
Группа, получающая новый препарат: пациент (1) 8; (2) 6; (3) 0; (4) 3; (5) 14; (6) 5; (7) 11; (8) 2
Группа, получавшая плацебо: пациент (9) 7; (10) 10; (11) 4; (12) 11; (13) 2; (14) 8; (15) 8; (16) 6; (17)1; (18) 5.
Какова меньшая сумма рангов в двухвыборочном тесте Манна-Уитни? Какая выборка пациентов обеспечивает это? Существенна ли разница на уровне 5%?
Ответы Гл. 10.pdf
Статистика рангов — Математическая энциклопедия
Статистика (см. Статистическая оценка), построенная на основе вектора рангов. Если $ R = ( R _ {1} \dots R _ {n} ) $
вектор рангов, построенный из случайного вектора наблюдений $ X = ( X _ {1} \dots X _ {n} ) $,
то любая статистика $T = T(R)$
которая является функцией $ R $
называется ранговой статистикой. Классическим примером ранговой статистики является коэффициент Кендалла ранговой корреляции $\tau$
между векторами $R$
и $ \ell = ( 1 \dots n ) $,
определяется по формуле
9{ п }
\влево ( я — п+
\фракция{1}{2}
\верно )
\left ( R _ {i} — n+
\фракция{1}{2}
\верно ) ,
$$
— линейная ранговая статистика.
Линейные ранговые статистики, как правило, просто построить с вычислительной точки зрения и их распределения легко найти. {2} \} $
{2} \} $
минимальна при условии, что $ H _ {0} $
верно, называется проекцией $T$
в семейство линейных ранговых статистик. Как правило, $ \widehat{T} $
приближается к $ T $
ну и разница $ T — \widehat{T} $
пренебрежимо мал как $ n \rightarrow \infty $.
Если гипотеза $ H _ {0} $
при котором компоненты $ X _ {1} \dots X _ {n} $
случайного вектора $ X $
являются независимыми случайными величинами, то проекция $ \widehat{T} $
$ Т $
можно определить по формуле
9{ п }
\ widehat {a} ( я , р _ {я} ) — ( п — 2 ) {\ mathsf E} \ {T \},
$$
где $ \widehat{a} ( i , j ) = {\mathsf E} \{T \mid R _ {i} = j \}$,
$ 1 \leq i , j \leq n $
(см. [1]).
Существует внутренняя связь между $ \tau $
и $\ро$.
В [1] показано, что проекция $ \widehat \tau $
коэффициента Кендалла $\tau$
в семейство линейных ранговых статистик совпадает с точностью до мультипликативной константы с коэффициентом Спирмена $\rho$;
а именно,
$$
\широкая шляпа\тау =
\фракция{2}{3}
\влево ( 1 +
\фракция{1}{п}
\справа ) \ро .
$$
Из этого равенства следует, что коэффициент корреляции $ \mathop{\rm corr} ( \rho , \tau ) $
между $\rho$
и $\тау$
равно
$$
\mathop{\rm корр} ( \rho , \tau ) = \
\ кв {
\ frac { {\ mathsf D} \ widehat \ tau }{ {\ mathsf D} \ tau}
«=»
\ frac {2 ( п + 1 ) } {\ sqrt {2 п ( 2 п + 5 ) } }
,
$$
, из чего следует, что эти ранговые статистики асимптотически эквивалентны для больших $ n $(
ср. [2]).
Литература
| [1] | Й. Хайек, З. Сидак, «Теория ранговых тестов», акад. Press (1967) |
| [2] | М.Г. Кендалл, «Методы ранговой корреляции», Гриффин (1970) |
Как процитировать эту запись:
Ранговая статистика. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Rank_statistic&oldid=51568
Эта статья была адаптирована из оригинальной статьи М.


 Они должны были бы получить ранги 4
Они должны были бы получить ранги 4
 главу 11).
главу 11).